Why Some Students Learn Faster

A hypothesis about teaching and learning

Students are different from one another in all sorts of ways. The overwhelming experience of teachers is that students need different things to learn. But why? What are those differences? Are there systematic ways that students are different, or is it all kindof random?

I have a hypothesis about one major difference between students. I don’t think this is the only way that students are different, but it’s an important one and has concrete implications for how we teach.

This post is based on a lot of research I’ve read, research on teaching as well as intelligence. But this isn’t a “research says” post. I’m connecting some dots, trying to take a few different threads and tie them together in a way that’s useful for teachers. This post is informed by research, but also by my experience as a teacher and my observations about what works and for which students. Here goes.

What Does It Mean To Be Smart?

We throw around the word “smart” in education. But what does it mean to be smart? The details are often glossed over. It’s easy to fall into a circular definition. Some students are smart because they do well in school, and they do well in school because they’re smart.

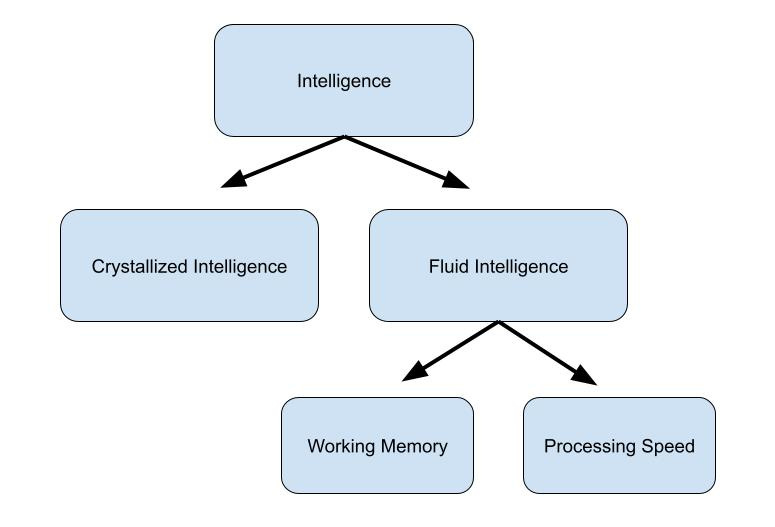
Researchers divide intelligence into two parts: crystallized intelligence and fluid intelligence. Crystallized intelligence refers to how much you know: knowing things makes you smarter. I’m going to put crystallized intelligence to the side for the moment. I’ll come back to it later, but for now crystallized intelligence is what we want for students. Fluid intelligence is a broad term for how well we can think and reason when we don’t have crystallized intelligence to rely on. There’s plenty of disagreement as to what exactly fluid intelligence means. I think conceptualizing fluid intelligence as some sort of vague measure of cognitive horsepower isn’t very helpful: we end up with “intelligence means being smarter” again which isn’t much use for teachers. In the debate about what exactly fluid intelligence means, two big components that most researchers agree on are working memory capacity and processing speed. Working memory capacity refers to how many ideas we can hold in our mind at once, and processing speed is a measure of how quickly we can think. Serious researchers suggest that those two may make up the vast majority of fluid intelligence. That’s my mental model for this post: some students have more working memory capacity and faster processing speed, others less working memory capacity and slower processing speed.¹ When we talk about students being more or less smart, we’re often referring to these differences.

I think this is a good mental model for teachers because it’s practical. In general, teachers have an intuition that some students are smarter than others. But what does that mean? If being “smart” means that some students will always achieve at a higher level, or other students can never learn a topic because it’s too abstract, we end up with self-fulfilling prophecies for which students will be successful in school. But thinking in terms of working memory and processing speed narrows in on specific, empirical elements of thinking and learning. I can see those differences in my students: all teachers can observe that some students are quicker thinkers, and some students can juggle more ideas in their mind at once. And we can teach in ways that mitigate those differences, that help all students learn.

I want to emphasize what this mental model doesn’t say. Both working memory and processing speed influence how new information comes into our minds. They don’t imply limits on long-term memory. All of the evidence we have suggests that, for all practical purposes, long-term memory is unlimited. For the vast majority of our students there is no hard ceiling on what they are capable of learning. Instead, there are constraints in terms of how new information comes in. I’ll return to this idea at the end of the post, but for now my mental model looks something like this:

I realize this image isn’t that great. The goal is to emphasize that working memory and processing speed act as a bottleneck between learning and long-term memory.

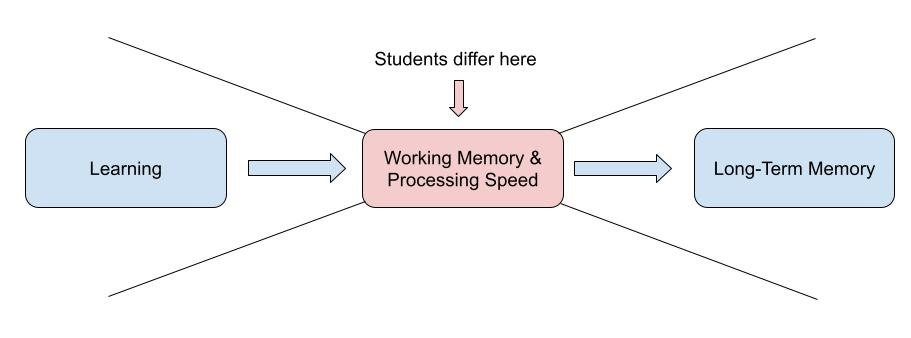
Let’s say you accept this premise: a major difference between students is fluid intelligence, which we can think of as working memory capacity + processing speed.² What does this mean for teachers?

Teaching

Having more working memory capacity and a faster processing speed makes learning easier. But it makes learning easier in very specific ways. I’ll repeat a quote I used in last week’s post. Talking about phonics instruction, Snow & Juel say: phonics is “helpful for all children, harmful for none, and crucial for some.”³ That’s the idea behind the teaching strategies I’ll share below. If you don’t use these, plenty of students will still learn. Teaching in this way won’t hurt any students with more fluid intelligence, but without using these strategies some students with less fluid intelligence won’t learn much at all.⁴

Check Prerequisite Knowledge and Reteach if Necessary

All learning builds on prior knowledge. Vocabulary, foundational skills like multiplication facts, concepts like the relationship between multiplication and division.

If students don’t have this knowledge, it’s harder to learn. But students with greater working memory capacity and faster processing speed can compensate: they are better able to quickly figure out a prerequisite skill and fill in those gaps as they learn. Students with less fluid intelligence have a harder time doing so. As teachers, we can mitigate this by thinking carefully about the prerequisite knowledge for each skill we teach, checking that students have it, and reteaching when necessary.

Time is a limiting factor here. We can’t take forever to reteach prerequisite knowledge. But in many cases, we can quickly remind students of the meaning of a vocab word or review a skill from a previous year that students are rusty on. Those quick tweaks can make a big difference in student learning. And when we have more time, there are often larger skills like math fact fluency that are worth reviewing and practicing.

Break Learning Down Into Small Steps

Whenever we teach, we ask students to make leaps from what they know to what we want them to learn. Students with more fluid intelligence can make larger leaps, moving from one idea to a much bigger idea. Students with less fluid intelligence struggle to make those large leaps, and learn more smoothly when learning is broken down into small steps.

My mental model here: students with more working memory capacity and faster processing speed aren’t actually taking larger steps. They are using their own cognitive resources to fill in those rungs and build the ladder as they’re climbing it.

However you think about it, the teaching tip is straightforward. Take complex ideas, break them into small, manageable chunks, and teach one chunk at a time. There are lots of ways to do this. Teachers can take big ideas and break them down into small steps. We can also modify tasks to focus on the most important pieces we want students to learn and reduce cognitive overload. We can use questioning to model the thinking we want students to practice. We can provide more and faster feedback. We can help students gradually apply what they know in different contexts. We can give extra support when we ask students to try more challenging tasks.

The details are tricky, and they depend on the specific learning objective, but there are always smaller, more manageable steps we can provide for students.

Connect New Learning to Prior Knowledge

Learning isn’t about jamming students’ minds full of facts. It’s about building schemas — connections between different ideas, abstractions that build on concrete examples, and mental structures that allow students to make sense of new information more easily.

One important element of learning is connecting what we want to teach with what students already know. Those connections help students to build effective schemas, and make learning stickier and easier to apply in new contexts.

Students with more working memory capacity and faster processing speed can often make these connections on their own. I see this all the time. Some students are constantly saying, “oh, this is like that other thing we learned.” Others struggle to make these connections on their own because they have less spare cognitive bandwidth.

That’s where teachers come in. Our job is to make these connections clear to students. To sequence concepts together to help students see the connections. To ask questions that get students thinking about similarities and differences. To highlight the underlying structures that tie ideas together, not just the surface details that make them look different. To help students see the patterns, relationships, and principles that make knowledge transferable rather than isolated.

Obtain a High Success Rate

Learning is harder for some students than others. That’s obvious to any observant teacher. And it’s harder for lots of reasons — attention, motivation, interpersonal conflicts, lots of other reasons. One reason learning can be harder is simply that, for students with less fluid intelligence, they have to think harder in school each day. They experience more cognitive overload, more stress on their working memories, more fatigue as they take longer to think through new ideas. The specific consequences depend on the student, but in many cases students with less fluid intelligence feel frustrated and dumb in school, and that fatigue creates negative feelings about learning.

One concrete way teachers can help is to support students with more practice until they reach a high success rate. A high success rate is important for learning: when students are reliably successful with a skill, it’s more likely they’ll retain what they’ve learned. But it’s also important for motivation. For students with less fluid intelligence, who feel more strain from learning and are more likely to become unmotivated, helping those students achieve a high success rate when learning new ideas helps to motivate them, helps them to see the progress they’re making and recognize that the effort they are putting in is going somewhere fruitful.

Provide Spaced Retrieval Practice

One confusing element of working memory and processing speed is that they aren’t numbers that are set in stone. The more we know about a concept, and the more fluently we know it, the less strain that concept puts on working memory. The more we know, the faster we can think. This is true across all contexts: we read faster when reading about a familiar topic. We speak more fluidly in our first language than a language we are learning. We write more coherently when we have a lot of knowledge to draw on. This brings us back to crystallized intelligence. Crystallized intelligence supports fluid intelligence. The more we know, the better thinkers we are. Students with a lot of fluid intelligence can get away with knowing less, and compensate for a lack of crystallized intelligence because they have more cognitive resources to draw on. Others can’t.

One of the most important things we can do for those students is to help them become fluent with the skills we teach that come up most often in the future. Fluency frees up cognitive resources for new learning. The best way we can help students become fluent is regular retrieval practice, and a spacing schedule that ensures students get retrieval practice at increasing intervals to improve long-term retention. Spaced practice helps students develop automaticity with the skills we want them to learn. That automaticity frees up cognitive resources for learning more abstract and challenging skills. Then we help students develop automaticity with those more challenging skills, and bootstrap upwards.

There’s again a time constraint here. We can’t provide unlimited practice for every skill. But we can identify the most essential content that will come up over and over again in the future, things like math facts in elementary school, one-step equations in middle school, and more, and practice those until students are automatic.⁵

Don’t Blame Students

I’ve encountered a lot of people who tell a similar story about their math learning. Math learning went fine until one specific point. Sometimes it’s fractions, or equations, or Algebra II, or calculus, or something else. And at that point they just got stuck. Math didn’t make sense any more. These people are often convinced that their brains are incapable of learning any more math. They locate the problem inside of their brain, rather than with the instruction they received.

The teaching strategies I described above are pretty common in elementary school. I bet plenty of elementary teachers reading this post are thinking, “yea of course, we do this every day, young kids need this type of teaching.” In middle school, it’s more hit-or-miss. Some teachers do all of these. But others don’t, and this type of teaching often isn’t a big priority. In high school this type of teaching becomes rare, and in college it’s more or less nonexistent.

So when I hear people talk about how they hit a wall and just couldn’t learn math after a certain point, my interpretation is that it’s not something innate in their brain, it’s a type of teaching that we stopped providing. We left gaps in prerequisite knowledge to fester. We stopped breaking learning into small steps. We didn’t make explicit connections with prior knowledge. We didn’t push for a high success rate. We didn’t provide enough spaced retrieval practice.

It’s easy to blame students when they don’t learn. They just can’t handle the material, or they’re not motivated enough. It’s easy to look at other students who are learning well with the same teaching and assume the problem is with the students and not with the teaching. But in many cases, what we’re seeing is the differential effect of the cognitive resources our students bring to the classroom. Sure, some students can learn without these strategies. But more students can learn with the right instruction.⁶

I don’t want to be unrealistic. There isn’t some fantasy world of equal outcomes for all students out there if we do a better job teaching. There are also lots of other differences between students that matter in addition to this mental model for fluid intelligence. But this mental model is one approach to shrinking the gap between our most successful students and the students who struggle the most in school.

This isn’t easy. These are all teaching strategies I’m constantly working on. There’s no instruction manual lying in the teacher’s lounge that says “here is how to break skill A down into X, Y, and Z,” or “here’s how to connect today’s lesson to what students learned last year.” It takes effort and trial and error. But over time, as I find new ways to put all of these strategies into practice, they make a bigger and bigger difference for students, and help students who often struggle find success.

I want to reiterate my thesis. My mental model is that in general, students are not very different from one another in their long-term memory. There aren’t major differences relevant to K-12 education in what most students are capable of learning. The differences lie in how students need to learn it. Fluid intelligence — like any other human trait — differs from one student to the next. The five teaching strategies I lay out above mitigate those differences. Not to zero, not so that every student magically learns everything we have to teach. But they narrow the differences between students and raise the floor, so more students can access the content we intend to teach. None of the strategies are easy. They take expertise, hard-won by teachers improving their practice. They take deep knowledge of that content we teach. But the more I work on these elements of my teaching, the more I’m convinced that with the right pedagogical tools we can do a lot to shrink the gaps in achievement between students.

1. This isn’t a post about where differences in fluid intelligence come from. At a basic level, these differences are the same as any other differences between humans: humans are diverse in all sorts of ways, and cognitive capacities are no different from any other human trait in that respect. But it’s worth noting that those differences are not evenly distributed. To be clear: there are plenty of rich kids who have less fluid intelligence, and plenty of poor kids who are brilliant and have more. I’ve taught both. But on average, there are differences between those two groups. This feels a bit controversial to say but it shouldn’t be surprising. The brain is an incredibly complex organ. We know a bunch of different ways that brain development can be interrupted. Exposure to lead or air pollution are just two common examples, and these types of environmental influences are much more common for people living in poverty. There are more that we understand, and many more that we don’t understand. I won’t go on too long about this except to say that if our goal is to close achievement gaps in education, we should focus on factors outside of school in addition to classroom teaching and learning.

2. I’m not an intelligence researcher. I’ve read a fair amount about intelligence. (If you’re looking for a quick primer, the book Intelligence: All That Matters by Stuart Ritchie is a good place to start.) One tricky thing about fluid intelligence is that it’s often divided into pieces that are kindof circular. Researchers will divide it into elements like abstract reasoning, problem solving, and cognitive flexibility. But those are hard to measure, and hard to disentangle. Working memory and processing speed are two things we know how to measure in education (and often do measure, especially when testing students for special education services). There are serious intelligence researchers who suggest that those two are the underlying basis for the rest of fluid intelligence. Others would disagree. Some might add attentional control or something abstract like problem solving or something else. I’ll just say that maybe this mental model of fluid intelligence = working memory + processing speed isn’t perfect, but I think it’s a good approximation that’s concrete enough to be useful to teachers, and it’s much better than the circular “smart because learning is easier, and learning is easier because smart.”

3. There’s one clarification I want to make on the idea of “helpful for all, harmful for none, crucial for some.” Using these five teaching strategies doesn’t harm anyone’s learning. But they do take time, and there is an opportunity cost to that time. Some students don’t need as much time checking and reteaching prerequisite knowledge, or time on retrieval practice, etc. Judging how much time to spend on these elements of teaching is a practical challenge and there’s no easy answer. This is where some folks will come in advocating for tracking, and I will direct you to my recent post on tracking which emphasizes again that there’s no easy answer.

4. These teaching practices are drawn in part from Rosenshine’s principles of instruction.

5. Something that drives me absolutely fucking crazy. I’ve heard a number of prominent edu-consultants in the math world brag about how they never memorized all of their math facts. First, I always wonder if they’re lying. Second, I bet they’ve memorized the vast majority. they know 3x5=15, but they’re a bit rusty with 7x8=56. Third, they often have multiple degrees and have led successful careers as teachers and then consultants. They have the cognitive resources to learn just fine while re-deriving 7x8 whenever they need it. That’s nice for them. But plenty of our students don’t. It’s a shame that “I never memorized all of my math facts” is an applause line at math education conferences, and it reflects a fundamental misunderstanding of what students need to be successful in math class.

6. Some people here will mention that there are students who have profound intellectual disabilities, whose learning needs are very different and who this argument doesn’t apply to. Sure, I don’t disagree. But the vast majority of students — including many with mild to moderate learning disabilities — can learn the vast majority of what we intend to teach them in K-12 schooling if we provide the right instruction. Again, I don’t want to be unrealistic, but I absolutely believe we could achieve far better outcomes than what we achieve now. I think many students who could see more success in school are let down because we see other students learning from the same instruction, assume the problem is with the student, and blame them for not making enough connections or not being motivated enough.