Explorations in Math Class
Quality over quantity
I won something called the Rosenthal Prize. You can read a bit about it here. It’s a prize for "Innovation and Inspiration in Math Teaching." The prize is sponsored by the National Museum of Math in New York City. Here’s a picture of me at the Museum last week:
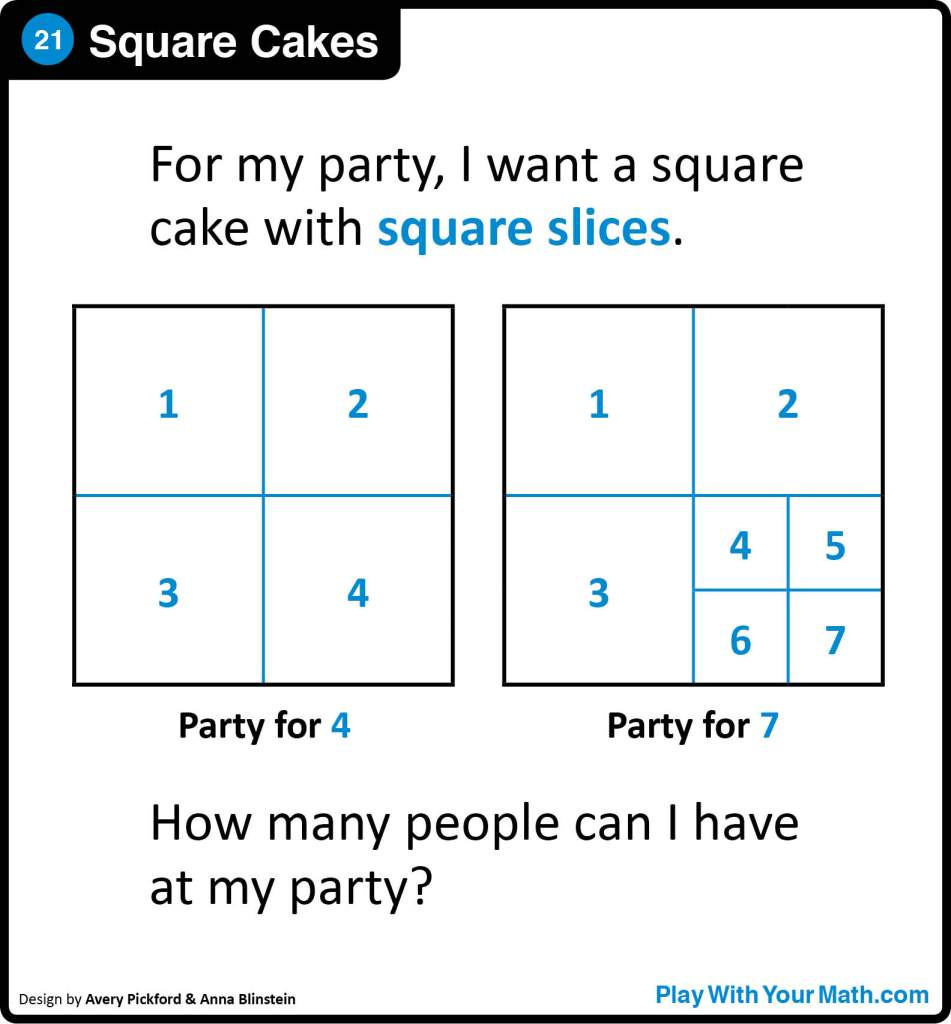
I won it for a lesson exploring a few problems with students. The main problem is this one, which I first learned about from the Play With Your Math site:
If you’d like a spoiler there’s one here.1
It's a ton of fun, a great problem for exploring math and accessible to a range of students. We start with a warmup looking at patterns in numbers, then walk up and down actual stairs to get a sense for the problem, then spend a bunch of time counting solutions on paper and looking for patterns. There’s an optional second day exploring a second, related problem about arranging dominoes in rectangles. You can see my full lesson plan here.
It feels weird to win something like this because I’m a regular teacher. If you wander into my classroom on a random day you'll probably see me doing regular teaching stuff and students learning regular math. I might be explaining a concept, or helping students practice a procedure, or struggling with classroom management in second period. I spend most of my time and energy as a teacher thinking about helping kids understand how to multiply integers, or to understand word problems about proportions, or to calculate percents.
But I do things like this sometimes, activities that are more open-ended and give students the chance to explore and look at math from a different perspective. I think these are important and I want to articulate how they fit into my teaching. If you want to see more of how I think along these lines, I wrote a post last year called "Math is Awesome" on this general topic.
Explorations
One argument in the ether of math education is that math is about exploration and discovering ideas and looking for connections. Therefore, the argument goes, we should teach students math through exploration and discovery and connections. I disagree with the second part. Teaching through exploration is really, really challenging. In my experience, that type of everyday teaching leads to some students feeling successful and confident in math class, and other students feeling frustrated. Math is largely cumulative. What tends to happen is that the students who have been successful in the past do well with exploration, and those who haven't been successful have a hard time. All of this retrenches the existing hierarchy.
I want students to experience exploration. Exploration is a major part of mathematics. I want students to get a glimpse of what that means. In my experience, the best way to do so is to focus on quality over quantity. My goal isn't to have students engage in exploration every day. My goal is that, when we do an exploration, as many students as possible have the chance to feel successful in the lesson.
If you look at my lesson plan, the piece I'm proudest of is the way the lesson is designed to be accessible for students. The problems are broken down into lots of pieces. There are lots of separate moments to figure stuff out rather than one big reveal. There are pieces of language and framing and facilitation that are designed to set students up for success.
It's interesting that this prize is for “innovation” in math teaching. My lesson uses well-known problems on a well-known topic. It's interactive in a way many math lessons aren't, but it's hardly unique. If it is innovative, it's innovative in the way that it works to make mathematical exploration accessible for as many students as possible. When I taught this lesson, a number of the students who enjoyed it, who contributed interesting perspectives or shared their thinking with the class, were students who are often disengaged in math class. The best math teaching isn't innovative because it's shiny and off-the-wall different. The best math teaching finds creative ways to help every student feel successful — especially students who have felt alienated in math class in the past.
One key to doing this well is using non-curricular problems for explorations. The problems in my lesson aren't tied to any standards or content. Students need some knowledge of addition to access them and not much else. Thees types of problems are absolutely where I think teachers should focus their energy if they want to do exploration well. Non-curricular problems level the playing field for students. If a problem doesn’t build on what students learned yesterday or last week, the students who felt frustrated yesterday and last week are more likely to give it a shot.
Problems
You might be thinking ok, that's nice, where do I get problems like this? The absolute best source is the Play With Your Math site. I can't recommend it enough. Here is a sample of a few more of their problems:
I like my lesson, of course, but you could do well with lots of questions on the site. Here are a few other thoughts on these problems:
The visual design is fantastic. I recommend scaffolding these for students by breaking them into smaller pieces, but PWYM is a great model for simple and thought-provoking visual design in education.
The problems invite tinkering and trying things out. They generally start with opportunities to experiment and see what happens. The most important part of an exploration is the first two minutes. Can students get started? Can they experience some success early on? PWYM problems often do that really well.
The problems lend themselves to extensions. As students figure things out there are new ideas to explore.
They're also just a ton of fun. I've enjoyed exploring many of these. I've come back to problems I've solved in the past and solved them again, or found new directions to explore.
To Summarize
Here's my thesis: Exploration and discovery are important parts of math. But they're hard to do well. Students deserve to experience exploration and discovery, so we should focus on doing them less often, with lots of supports so more students feel successful. A good strategy is to pick non-curricular problems every once in a while, break them into small pieces, and scaffold them so as many students as possible can access them. Doing an occasional exploration well is better than doing them poorly every day or every week.
Misc
Below are a few more miscellaneous thoughts on the prize and the process:
I feel like a complete fraud winning this. It feels fake. I’m a regular teacher, why is my lesson the winner? I don’t say that so you feel sorry for me, just to emphasize that if you’re thinking about applying you should! Even if it feels like you could never win! Applications are open now.
I’ve taught a few different versions of this lesson a few different times and they didn’t go perfectly or anything. I had to videotape one for my application. First period went pretty well, second period was a bit of a mess, third period was fine. That's how these things are.
I revised the lesson plan after the video, and again after some feedback from the committee, so the final version is two stages removed from the last version I taught. Spending that much time working on a single lesson is a cool experience. Also, the feedback from the committee was really helpful. I'm looking forward to teaching it again with the most recent edits.
Finally, I did some googling of past prize winners. In recent years a large majority are either outside k12 education (professors, math outreach, etc) or private school teachers. I don’t mean to criticize anyone specifically, I’m glad so many people are interested in crafting great math lessons. I used to work at a private school. But I would love to see more public school teachers represented.
Scroll down if you’re sure you want a spoiler:
The answer is the Fibonacci sequence






A thoughtful post as usual. In terms of exploration, I’ve found it workable for students to do short explorations at least once a week.