Working Memory Overload

A few examples of working memory overload in action

Working Memory

Working memory is where thinking happens. One of the striking features of human cognition is that we can only hold a few ideas in our mind at once. We can know lots of things — capitals of states and countries, how to solve equations, the meanings of tens of thousands of words, the names and faces of thousands of people. All that is stored in long-term memory. But at any time, we can only draw on a few pieces of knowledge to hold in our mind and think with. That limitation is the key feature of working memory.

Before reading further I recommend taxing your working memory for a moment to experience what it feels like. Here is a link to a simple working memory test, trying to remember a string of digits. Try it for four digits. Almost every human will find this task simple. Then try it for ten. Very few humans without memory training can do this consistently. I often think I'll be able to remember all the numbers and then make mistakes. That’s what it feels like when your working memory is overloaded.

There is disagreement about the exact number of things we can hold in our minds at once. Seven is often cited as the capacity for simple tasks like remembering a string of digits, but for more complex ideas it is lower. Some studies suggest the limit is as low as two or three ideas a human can hold in their mind at once without introducing errors or needing to refresh an item.

You might be wondering, what do I mean by an item? This is the cool part. Our brains don't remember stuff as random disconnected bits. Instead, we organize our long-term memory into what cognitive scientists call "chunks." Here's an example. If I give you ten random digits to remember you will almost definitely be unsuccessful. But if I give you the digits 20082012201620202024 and point out that those digits represent years, you will probably be able to remember them without a problem. If you are from the US it will be even easier — those are presidential election years, beginning with Obama's first election and ending with the current year. Grouping digits into chunks and giving those chunks clear, connected meaning makes it much easier to remember digits, so that suddenly you can hold 20 digits in memory without any trouble.

The key idea of chunks is that you get more working memory space "for free." If I want to know 4 x 3 and I have to think ok, 3, 6, 9, 12, that consumes a bunch of my working memory. If I have a chunk in long-term memory for 3 * 4 = 12 that consumes fewer resources, leaving those other resources for other parts of a problem.

Teaching

Why should teachers care? I see working memory overload in two different contexts. I think it’s worth getting specific about exactly what working memory overload looks like and how it affects students. First, working memory overload leads to mistakes. Second, working memory overload interferes with learning. I want to give two examples of each to explore exactly what happens in these situations.

Mistakes

When working memory is overloaded people make mistakes. This might seem obvious but it's worth looking under the hood at how this happens. Mistakes sometimes come from counterintuitive places.

Let's say a student is solving this problem:

The radius of a circle is 3 inches. What is its circumference?

The student thinks ok, the radius is 3 inches. What's the formula for circumference again? Ok I think it's pi times diameter. What's pi again? 3.something, what was it, wait I remember Jimmy saying it, hang on I need to look in my binder. Ok it’s 3.14. So pi times diameter, 3.14 * 3, grab a calculator, 9.42.

It's worth unpacking a specific moment there. First the student is holding "radius = 3" in their mind. Then they add "circumference is pi times diameter." So far so good. Then they try to remember what pi is equal to and they need to do some searching. That's where working memory overload happens. They can't hold everything in their mind, so "radius = 3" starts to fade, the same way those digits in the digit span test fade from your mind. If this student had a solid chunk in long-term memory that pi = 3.14 they might have avoided that mistake — thinking “pi times diameter” is the same as thinking “3.14 times diameter” if you have a solid chunk for pi in memory. This student also doesn't have a solid chunk for radius * 2 = diameter — if they had that chunk solidly in long-term memory when they first saw the problem they would get diameter = 6 "for free."

This is an interesting example to me because a teacher could easily draw the wrong conclusion. One conclusion is that the student should practice converting between radius and diameter. That's a reasonable next step. Another conclusion is that they should show their work. Also reasonable. Showing work is a good strategy to deal with working memory issues in general. But very few teachers in this situation would say to themselves "this student should practice retrieving pi = 3.14." That piece is hidden. And the key here is that committing pi = 3.14 to memory is pretty easy. The teacher could drop a few question in Do Nows at the start of class asking what pi is. A bit of regular retrieval practice makes a big difference. The lesson here is that when students don't have solid chunks in long-term memory they make mistakes, and the causes of those mistakes are often tricky to identify.

That example is a bit procedural. Kids should learn how to find circumference but maybe you don't think that’s a very important part of math, and you’d rather focus on problem solving. Here’s a problem-solving example.

Four 4s is a popular problem-solving activity that many teachers use at the start of the year. The challenge is to find as many numbers as possible using expressions with exactly four 4s and any operations students want. They might do 44 / 4 + 4 or 4*4+4+4, and so on. A common way to do it is to have students find expressions for different numbers and see how many numbers the class can find collectively.

Imagine a student trying to find a number. They start by doing 4 * 4. They don’t know what 4 * 4 is. They think to themselves, ok what's 4 * 4? 4, 8, 12, ok it's 16. 16 + 4 = 20. I got 20!

The mistake here is that while their working memory was taxed skip-counting to find 16, they forgot that they had only used two 4s.

A teacher might respond to this by suggesting the student show their work. Not bad advice. But a better way to help this student is to help them remember that 4 * 4 = 16 from memory, to build a solid chunk of 4 * 4 = 16 that doesn't consume extra space in working memory by having to skip-count.

Learning

Those first two examples have to do with mistakes. That's one category where working memory plays a role in school. But those are honestly the less interesting ones to me. More interesting are situations where a student might not make a mistake at all, but they don't learn something because they don't have solid chunks in long-term memory and consume valuable working memory resources when they shouldn't need to.

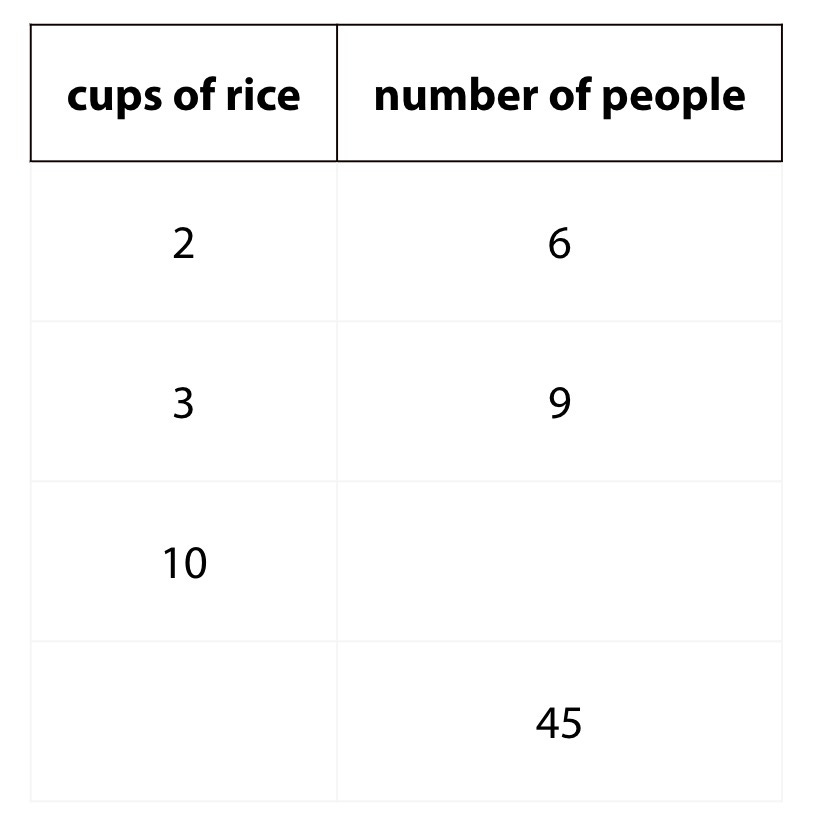
Below is a task to introduce the idea of a proportional relationship.

Something I want students to understand about this relationship is that, no matter what the specific numbers are, you always multiply the number of cups of rice by 3 to figure out how many people you can feed. I want students to understand that this property is the key characteristic of a proportional relationship. In this example, 2 x 3 = 6, and 3 x 3 = 9. But if a student doesn’t know those two multiplication facts — if they need to consume working memory figuring out what 6 / 2 is, and then again figuring out what 9 / 3 is — they won’t have space remaining in working memory to process the idea of a proportional relationship.

Here’s a second example. One of the trickiest ideas to understand in 7th grade math is the idea that when solving an inequality, multiplying by a negative number flips the inequality symbol. Here’s a series of examples I use to help students understand that idea. 3 < 6. And if I add 2 to both sides, 5 < 8. If I subtract 3 from both sides, 2 < 5. If I multiply both sides by 2, 4 < 10. The purpose of these examples is to illustrate that, for positive numbers, the operations we use on inequalities work the same way as with equations. But what if I flip the sign? 4 < 10. Is -4 < -10? It’s not, and that example can help to illustrate the idea that the inequality sign flips when multiplying by a negative number. But here’s the thing. To understand that example, you need to know two things without having to think about them. You need to know the meaning of the < symbol, and to be able to visualize positive and negative numbers on a number line. If, when I ask whether -4 < -10, you need to consume working memory to figure out where those two numbers are on the number line, or figure out whether that symbol means less than or greater than, you won’t also be able to hold the purpose of the example in your mind and understand what it’s trying to illustrate.

In both of these situations, a student experiencing working memory overload doesn’t make a mistake. They might be able to figure out everything in both situations — maybe using skip-counting to figure out those multiplication/division facts, and drawing out a number line and using a memory device to evaluate the inequality. But the working memory resources that they consume mean the student loses the forest for the trees, and they spend their time thinking about 6 / 2 or -6 < -15, rather than the idea of a proportional relationship or the rules for solving inequalities.

Working Memory is Counterintuitive

One key idea here is that working memory is counterintuitive. It fools teachers because when working memory is overloaded we can’t peer into a student’s mind and see exactly what they are thinking about, what pushed them over the edge, which moment they lost the thread of the lesson. When students make a mistake, the mistake might not be related to the part of the problem that overloaded their working memory, leading teachers on a bit of a wild goose chase. When learning something new, students might seem to understand every step individually, but use so much working memory on each step that they don’t make the larger connections we want them to remember. And on top of all this, teachers struggle to empathize with what students are experiencing because we typically have that foundational knowledge well-chunked in long-term memory and our working memory isn’t taxed by the same things that tax our students’ working memory.¹ The longer I teach, the more time I spend figuring out all those little things that make it harder for students to learn, all the little things that consume working memory, and helping students move that knowledge into long-term memory.

A final note. Two of the four examples I gave involved knowing multiplication facts. Fact automaticity is a common piece of knowledge that is one component of a larger problem, and can consume more or less working memory resources depending on whether students have the answer chunked. Knowing math facts is really important. There’s other stuff besides math facts that taxes working memory, but students don’t need to be automatic with every little thing. Some pieces of knowledge come up more often than others. We should identify the highest-leverage skills and practice them a lot so students don’t have to think about them. Not all math concepts are equally valuable. Mixing in regular practice on those key skills will pay huge dividends down the road.

1. Of course, teachers' working memories are taxed by other things. Right now for some reason my students love hot wheels. My working memory is taxed keeping an eye out for hot wheels, asking students to put them away, and keeping track of who I’ve already asked to put their hot wheels away and just taking those. I have a nice green Lambo now!