Learning That Doesn't Stick

Dissecting a moment of teaching and how it connects to memory

This video has been bouncing around the internet:

I don’t want to get into the “is AI good or bad for teaching" thing; this video is a good example of a teaching move that doesn't work very well.

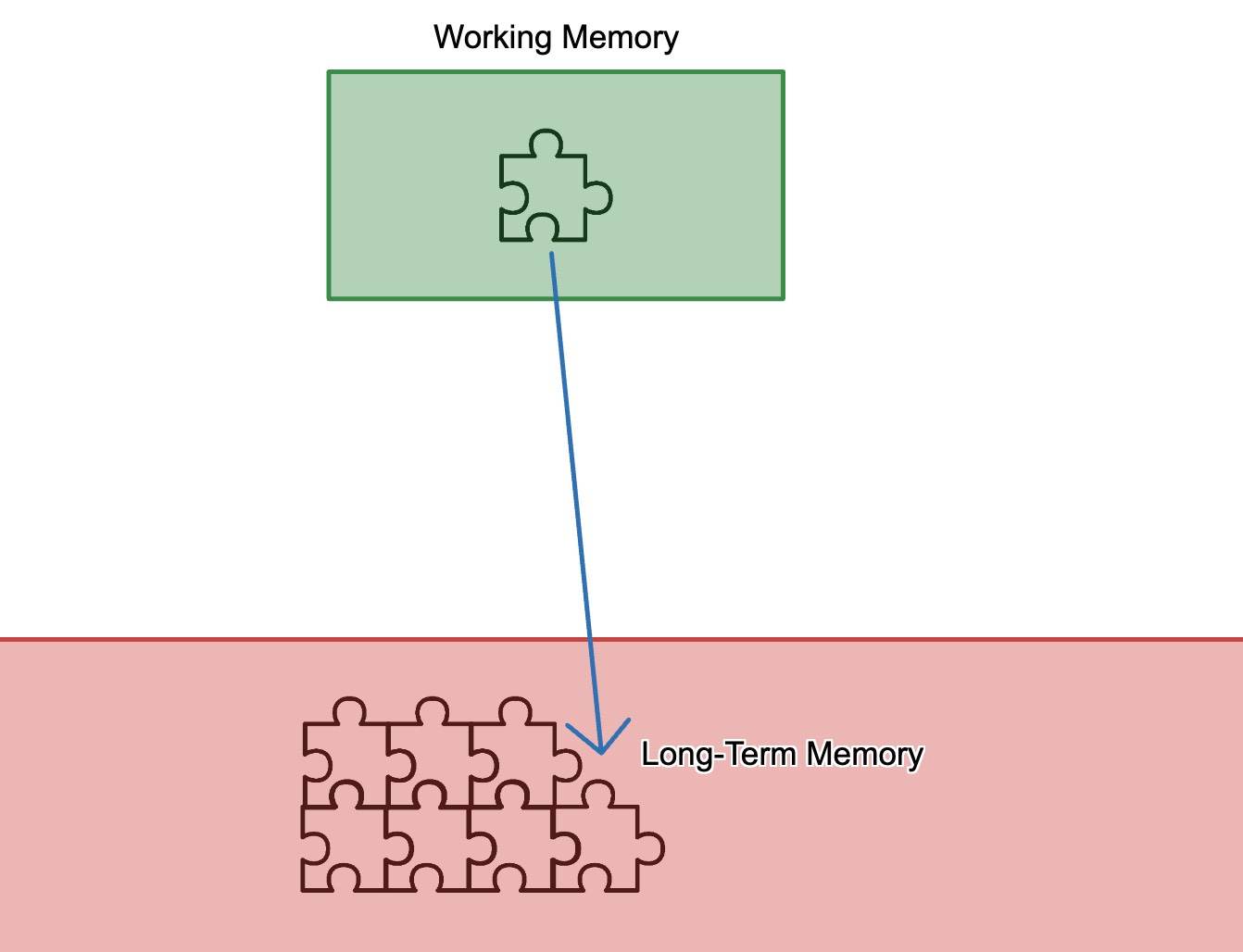
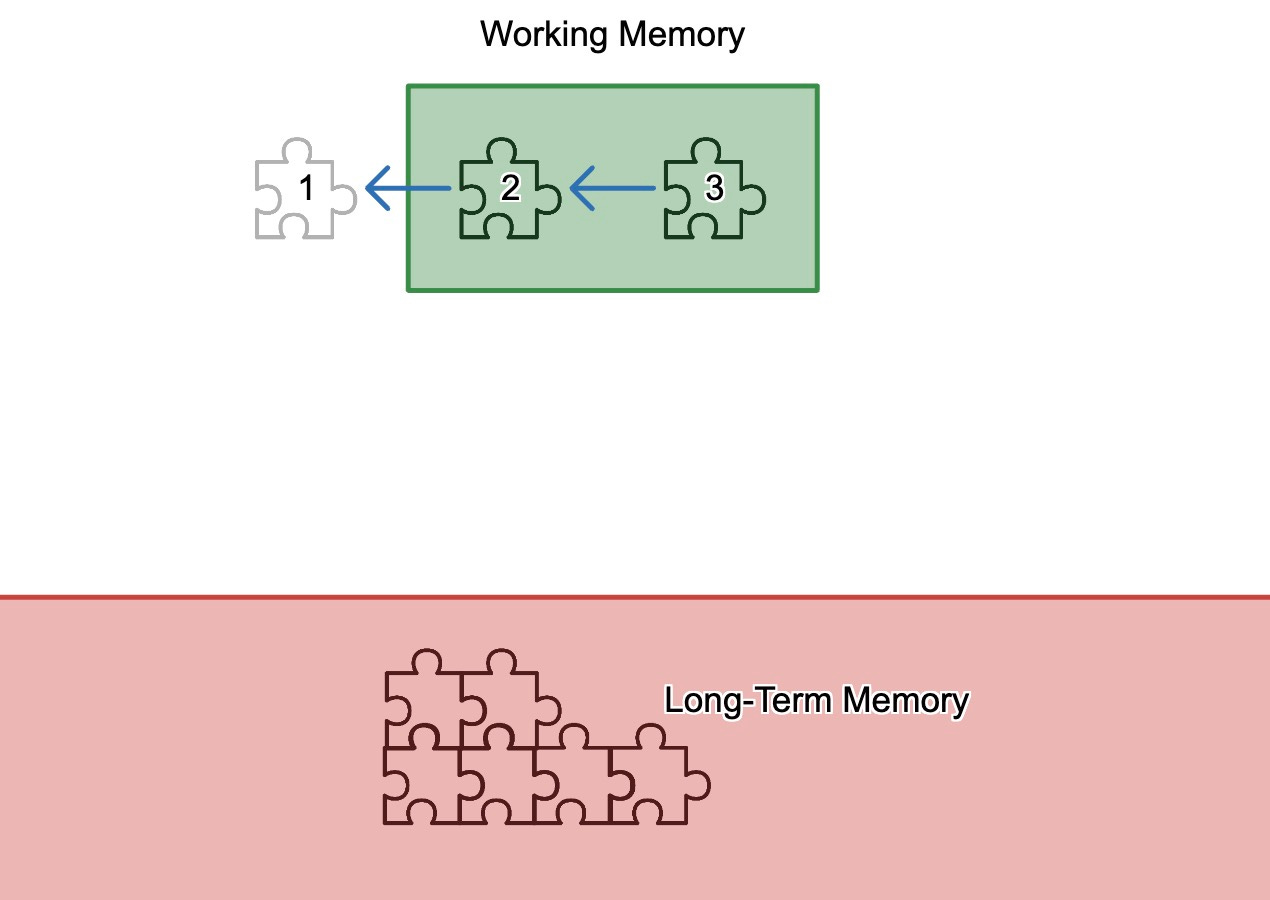
First, a quick idea about learning: learning sticks best when it is connected to stuff you already know. It looks something like this.

Working memory is where thinking happens. We learn something when we think about the thing, and think about how it's connected to what we already know. Long-term memory is sticky; the more you know, the easier it is to learn new things. This is often where that “a-ha” moment comes from: in many cases, that’s the feeling of figuring out how something you’re trying to learn fits into your current knowledge.

Back to the video. In the video, GPT-4o is talking Imran Khan through a problem about finding the sine of an angle in a right triangle. First, the AI asks Imran to identify the opposite, adjacent, and hypotenuse. Imran gets it wrong and misidentifies which side is the hypotenuse. You can see this around 1:00 in the video. The AI clarifies that the side he identified is actually the adjacent side and offers the definition of hypotenuse. Imran then identifies the hypotenuse correctly, the AI guides him through the formula for the sine of an angle, and he finds the sine of the angle.

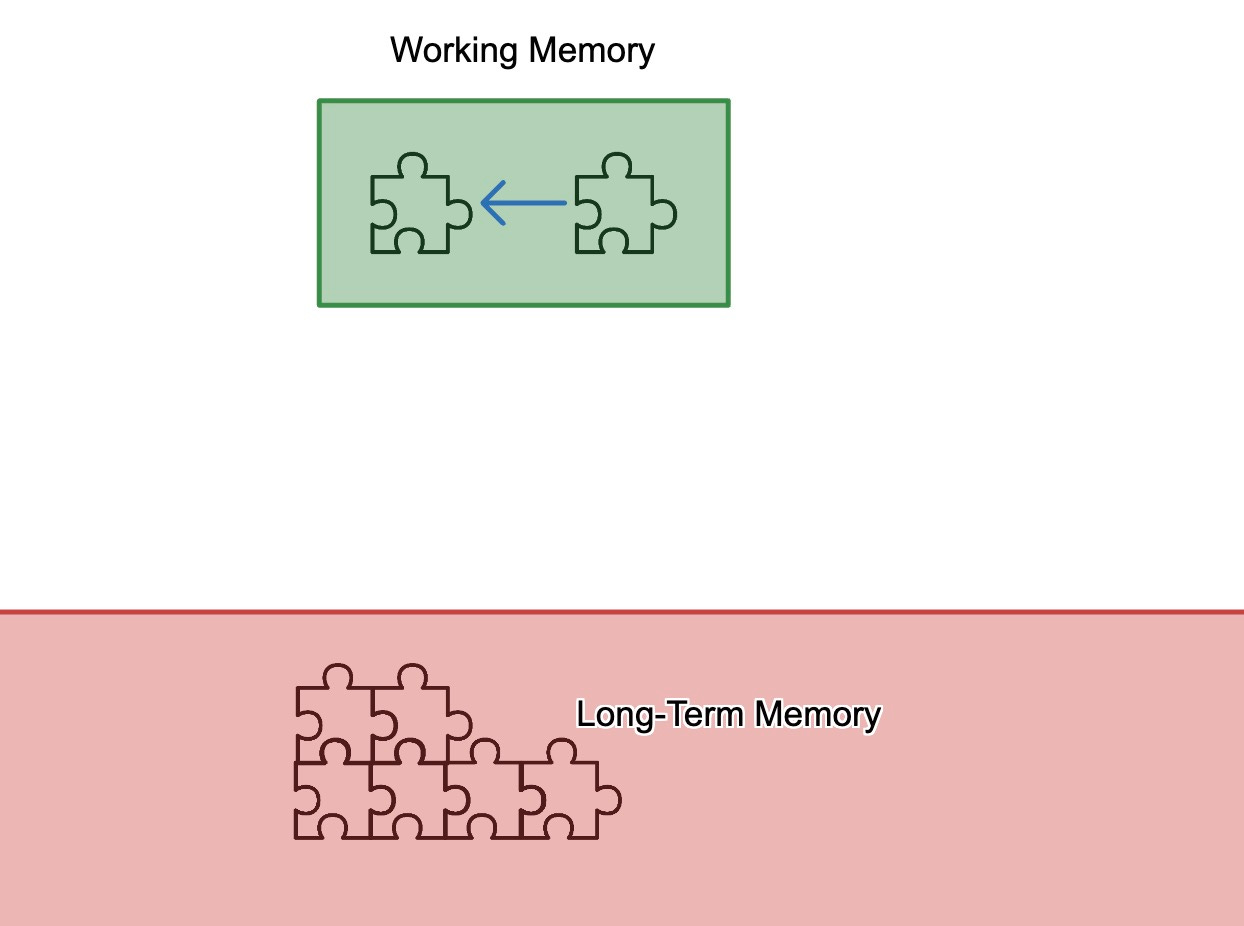
Forget about the AI for a second. I think a lot of teachers would see this as pretty good questioning!¹ But there's an issue here. If a student doesn't know what the adjacent, opposite, and hypotenuse mean, you're actually trying to teach two things at once. First, you're teaching adjacent, opposite, and hypotenuse, then you're teaching how to find the sine of an angle. Returning to the diagram from before, it looks something like this:

If a student doesn't have that prior knowledge in long-term memory, what they're learning about finding the sine of an angle isn't going to stick very well. The tutor doesn’t take any time to connect the opposite/adjacent/hypotenuse idea to anything the student already knows or have the student practice it to solidify it in long-term memory.²

There's a conflict in moments like this between helping a student solve a problem and helping a student learn something. If my goal is to get the student to the end of the problem then the questioning here works well. If my goal is to get the student to learn something, I need to pause. Once I realize the student is shaky on opposite/adjacent/hypotenuse, the best thing to do is to push the problem to the side and spend a few minutes applying those ideas to some new triangles. Maybe bring in the Pythagorean theorem — while it's not strictly necessary for problems like these, connecting to the Pythagorean theorem is a good way to draw on what a student hopefully already knows and help that opposite/adjacent/hypotenuse language stick.³ Then apply it to a few more right triangles with different shapes and facing different directions. Now, once that language is more firmly anchored in long-term memory, it's a good time to return to finding the sine of an angle.⁴

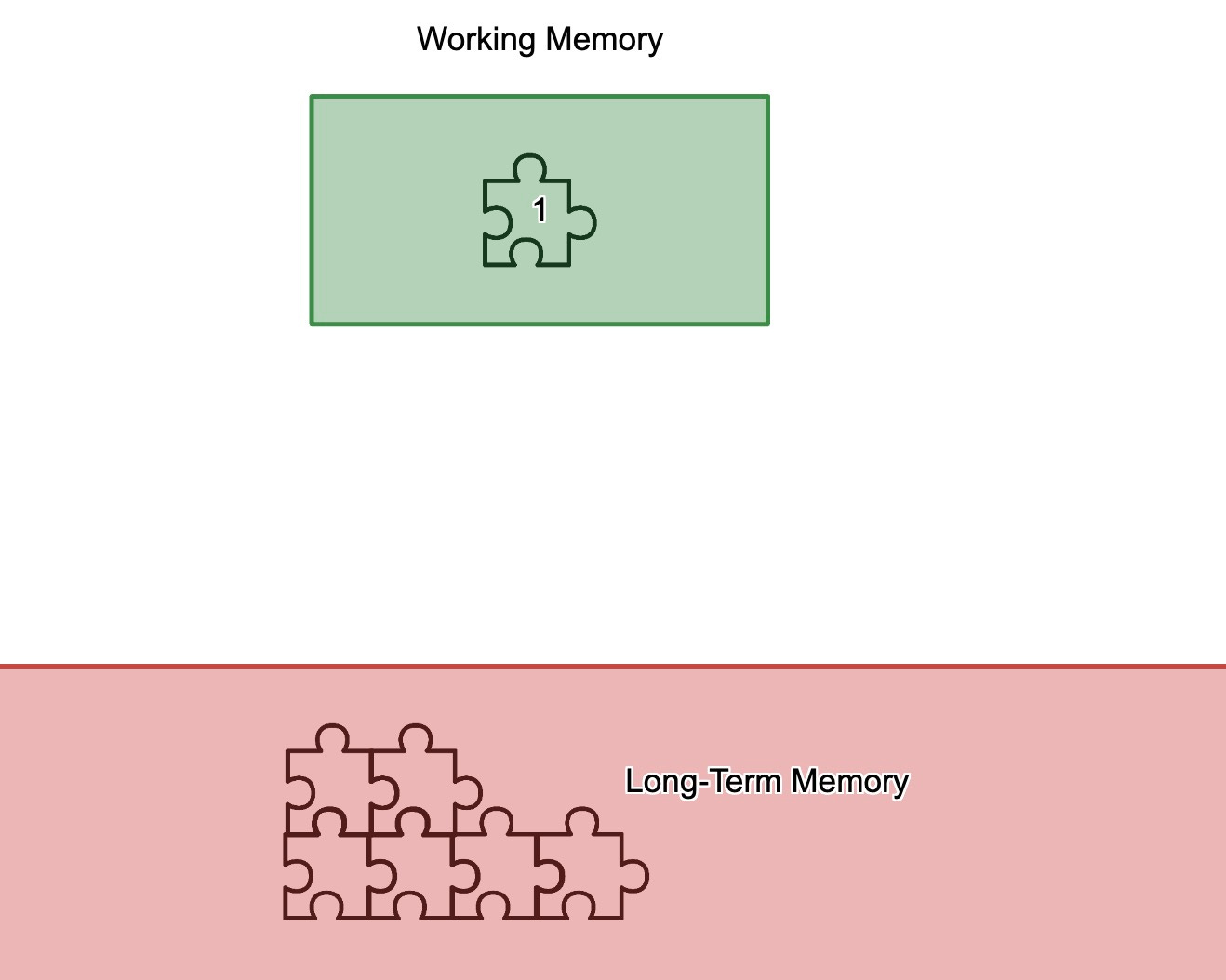
I don't know what to call this teaching mistake, but one challenge is that it can provide the illusion of learning. In some cases it looks like this:

You teach a student thing one.

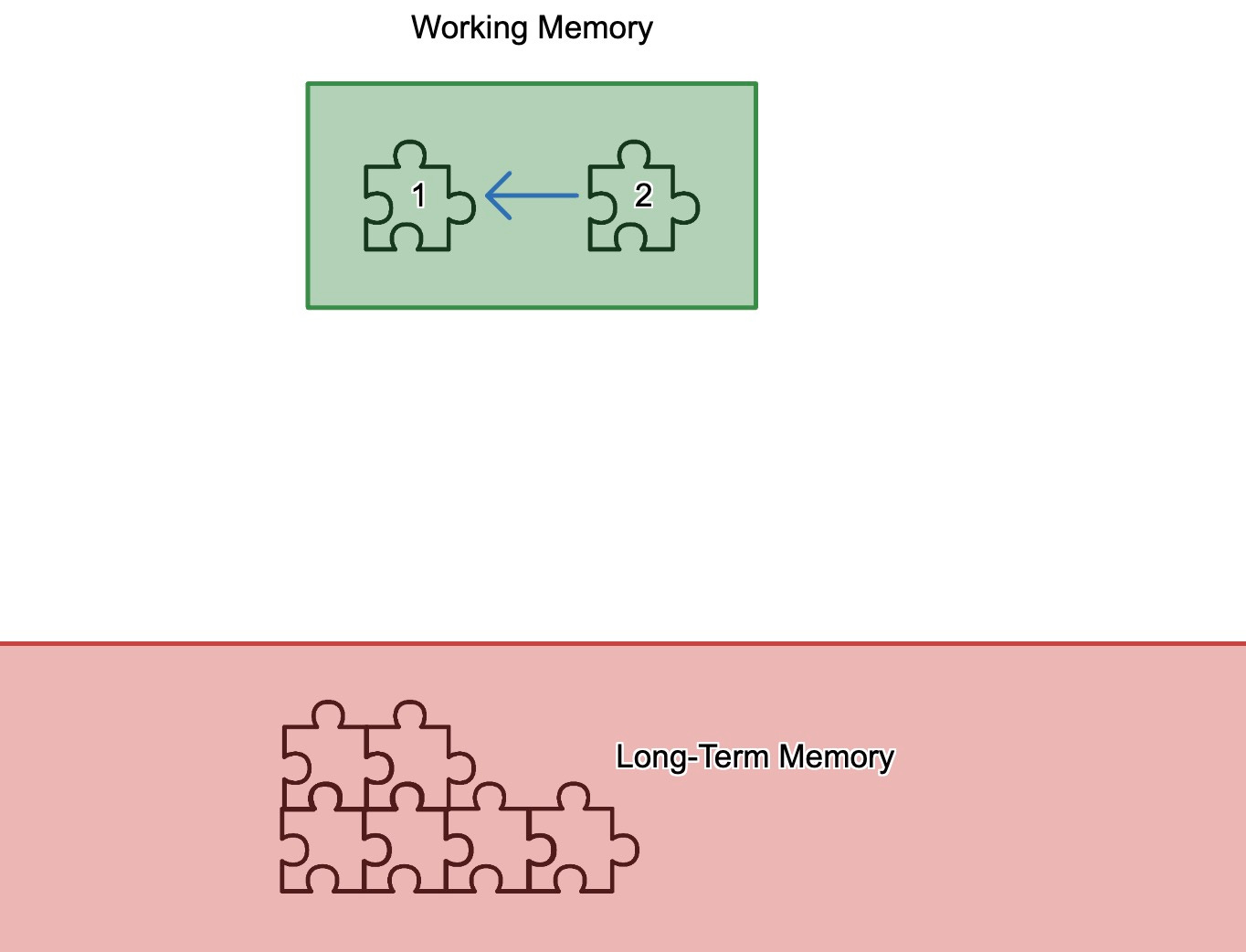
Before spending time connecting that to long-term memory, you teach thing two that relies on thing one.

The student feels like they’ve learned it! They’re holding both things in their mind and it makes sense. Then you teach thing three that relies on thing two.

The mistake here is not taking time to move each of these to long-term memory — thinking about how it's connected to what you already know, applying it in a few different situations, doing some retrieval practice. Working memory is limited. Learning fades away without an anchor in long-term memory. It can seem like learning is happening, though! In your mind, each connection feels clear in the moment. In that last diagram, the connection between 1 and 2 feels clear and logical, then the connection between 2 and 3 feels logical! Yet the next day the learning has evaporated. The key is to slow down and make sure that whatever I want students to learn rests on a solid foundation in long-term memory for it to stick to.

1. GPT-4o makes a few other errors as well, there is a good summary here.

2. A reasonable criticism of my argument is that there isn’t a sharp division between working memory and long-term memory. Everything we think about in working memory creates some sort of trace in long-term memory. This isn’t a perfectly scientifically accurate metaphor for learning, but it is a useful metaphor for learning and I think the broader conclusions hold up.

3. I’m taking a kindof “zoomed in” view of learning, focusing specifically on teaching how to find the sine of an angle. Another aspect of teaching here is thinking about why someone might care about finding the sine of an angle, thinking about how this topic fits into the larger story of math, and connecting it to other math topics the student has already learned. Those are all ways to connect the learning to long-term memory. They’re important! It didn’t seem fair to go on about this “zoomed out” perspective since we get such a small slice of learning here, but this zoomed out stuff is important too.

4. Even better is to identify smaller building blocks like this and work on them a day or several days before so that learning has more time to consolidate in long-term memory.