Fuzzy Math

All the math that's not school math but is still worth learning

One standard I always enjoy teaching is the triangle inequality theorem. The theorem says that for every triangle, the two smaller sides must add up to more than the biggest side. In precise terms, for all triangles a + b > c where a <= b <= c. Here's a nice picture:

It's a fun topic to teach. First I try to give students a basic intuition for the idea that some triangles are impossible. Then we get more precise in how students can articulate that condition.

What Is School Math?

There's a subset of school math that is very practical. I teach percent increase and decrease, which are useful in everyday life. Most adult humans are expected to understand how taxes and discounts work. There's another subset of school math that leads toward other, higher math. I also teach two-step equations. If I'm being honest, many of my students will rarely or never use a two-step equation in their lives beyond school. But learning two-step equations is a rung towards lots of higher math. It keeps doors open for future opportunities. There's also a third category: math for the sake of math. The triangle inequality theorem falls in this category. It doesn't lead to much future math. It's not useful in the "real world." But it's worth learning. It's great abstract thinking. It's one tiny element of showing students what math can do, demonstrating the power of reasoning and abstraction.

But why the triangle inequality theorem? Why not other math? I don't think there's a particularly good reason. And there's a lot of math out there.

I teach the 7th grade math standards, as I am required to. But I also carve out a bit of time for what I call fuzzy math. Here's the premise: some of the choices we've made in the standards are arbitrary. Why the triangle inequality theorem and not something else? There's a lot of other math out there. And a lot of it is more fun, more light-hearted, and more accessible than the school math we've chosen.

Examples

Here are a few examples of fuzzy math I've used this year:

Learn a bit about fractals and Sierpinski triangles, then draw our own Sierpinski triangles, color them in, and tape them up on the wall in a giant-meta-Sierpinski triangle.

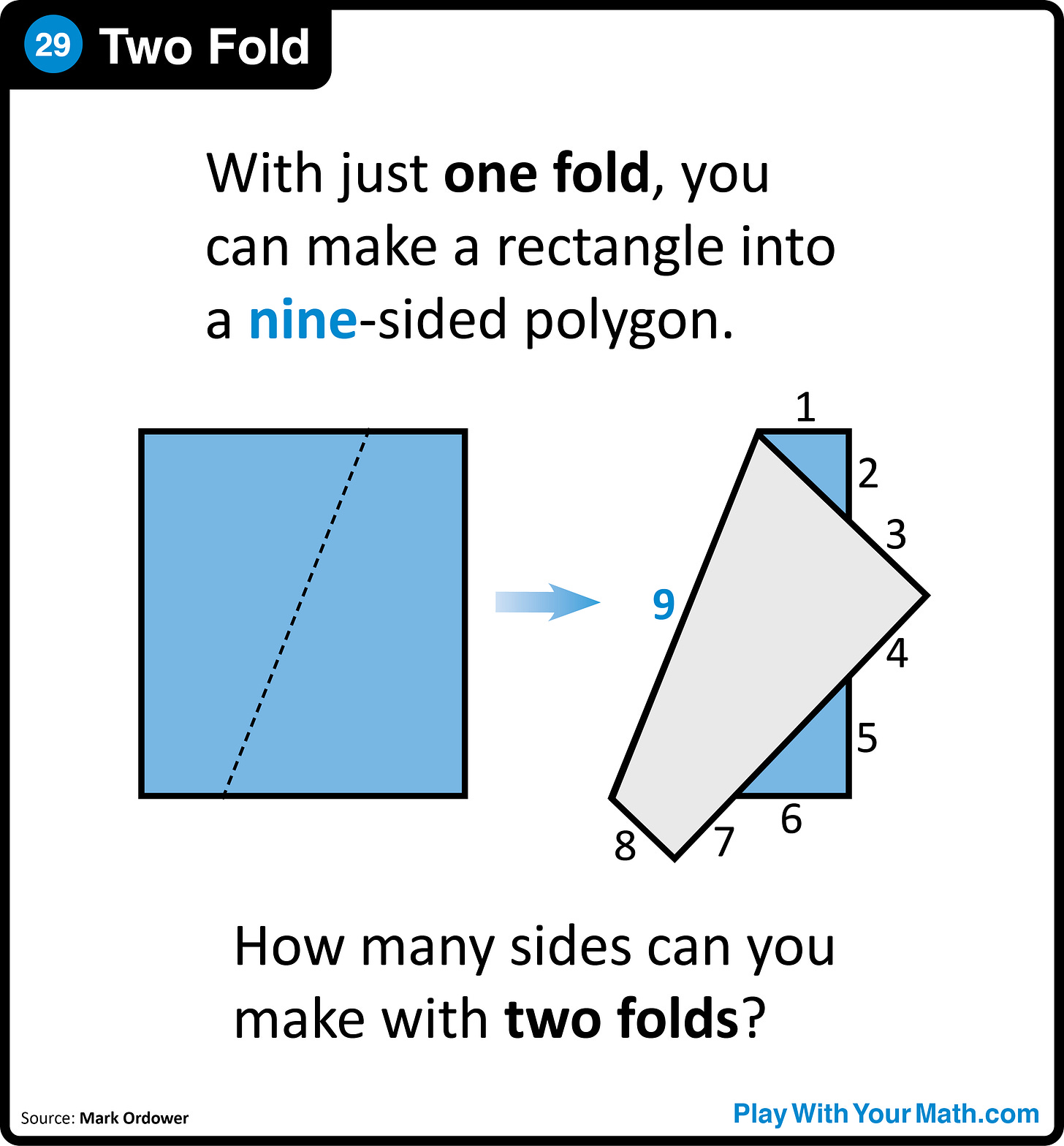
Learn some games from the great book Math Games with Bad Drawings.¹ Here's an example:

Learn the basics of Sudoku or other puzzles.

Do a longer exploration of a problem, like this problem I wrote about here:

Learn how to solve one side of a Rubik’s cube.²

Those topics can all be fun in their own right, and they all connect with different mathematical ideas that are worth learning.

One Rule

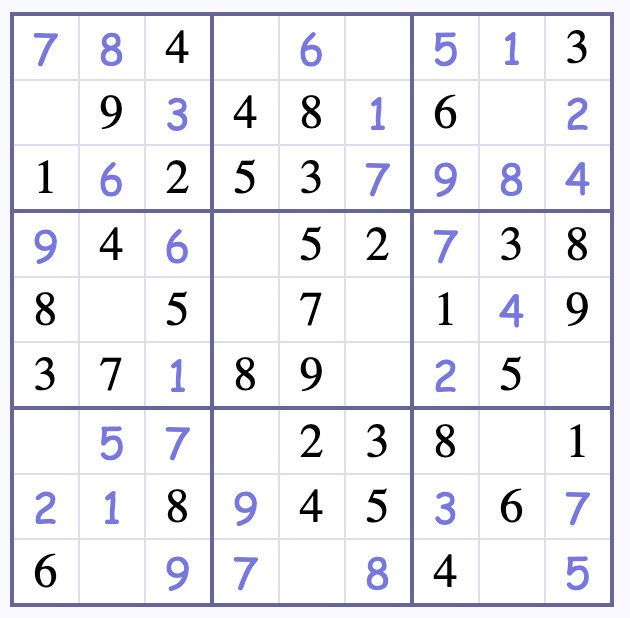
There's one important rule I have for fuzzy math: this is still teaching. For instance, if we're doing Sudoku, I don't just throw some Sudoku puzzles in front of students. I break it down into small pieces. I start with some nearly-solved puzzles like this one.

I work with students on the micro-elements of strategy. Students build confidence and gradually try harder and harder puzzles. If we're playing a game I start with a basic intro, then give students some scenarios and help them learn strategy, and then get into more unstructured play. It's the same principle I use when teaching anything else: break a topic into small chunks, practice the chunks, help students gain confidence, and gradually increase the difficulty. That means I don’t bounce around too much from one fuzzy math topic to another. I pick one topic and stick with it long enough that students learn something and get good at it.

The big advantage of fuzzy math over school math is that fuzzy math often has fewer prerequisites. A lot of school math builds on other school math. There is a group of students who continually feel behind and struggle with school math. One benefit of fuzzy math is giving those students a chance to succeed.

How Much?

How much of math class should be fuzzy math?

If you tell me that math class should be 100% school math and 0% fuzzy math, I disagree. What makes school math so special? No fuzzy math at all? No way.

If you tell me that math class should be 50% school math and 50% fuzzy math, I disagree. Fuzzy math often feels fun, and maybe you can convince yourself you're actually teaching problem solving or whatever. But that sounds like low expectations. School math is worth learning. If someone put me in charge of what students learn in school math I would have plenty of tweaks, but the basic structure seems fine to me. It's not easy for many students, but that's part of what makes it valuable. Students can do hard things.

I don't know what the exact right ratio is. Right now I’m at about 5% fuzzy math, 95% school math. It changes a bit as I tweak things, it shifts depending on the time of year, but 5% is a decent estimate. Sometimes that means a full class period. More often it’s a series of 5-15 minute chunks building over multiple days, in parallel with the regular school math we’re learning.

I'm lucky that I have a decent amount of autonomy in what I teach. Not all teachers have that. (Not even all teachers at my school have that.) But I think there's a serious argument for a little bit of fuzzy math in every math class. Education is important, school is valuable, teaching matters. But let’s not take ourselves too seriously, and do some fuzzy math every once in a while.

1. I highly, highly recommend purchasing this book. Most of the games can be played with pencil, paper, and regular household items like paperclips.

2. I have no idea how widespread this is, but where I live there are a few local organizations and companies that offer small grants for teachers. I can request $150 for a class set of Rubik’s cubes or similar materials and often get it. I’d recommend asking around if you’re looking to find resources for something like this.