A Critique of the Expertise Reversal Effect

Or, why experts vs novices isn't a helpful distinction

Expertise Reversal

There's a strand of research called the "expertise reversal effect" that's referenced a lot among education research types. Here is the original paper by Kalyuga et al. The core claim is that novice learners who have less knowledge of a subject benefit from high levels of guidance, for instance worked examples. Meanwhile, expert learners who have more knowledge benefit more from problem solving activities.

I don't like the framing of experts and novices. How are teachers supposed to determine who is an expert and who is a novice? The research isn't very helpful, it talks about schemas and redundant information and I find it very opaque. It would be easy to conclude that students are novices because they're students, so teachers should never use problem solving.

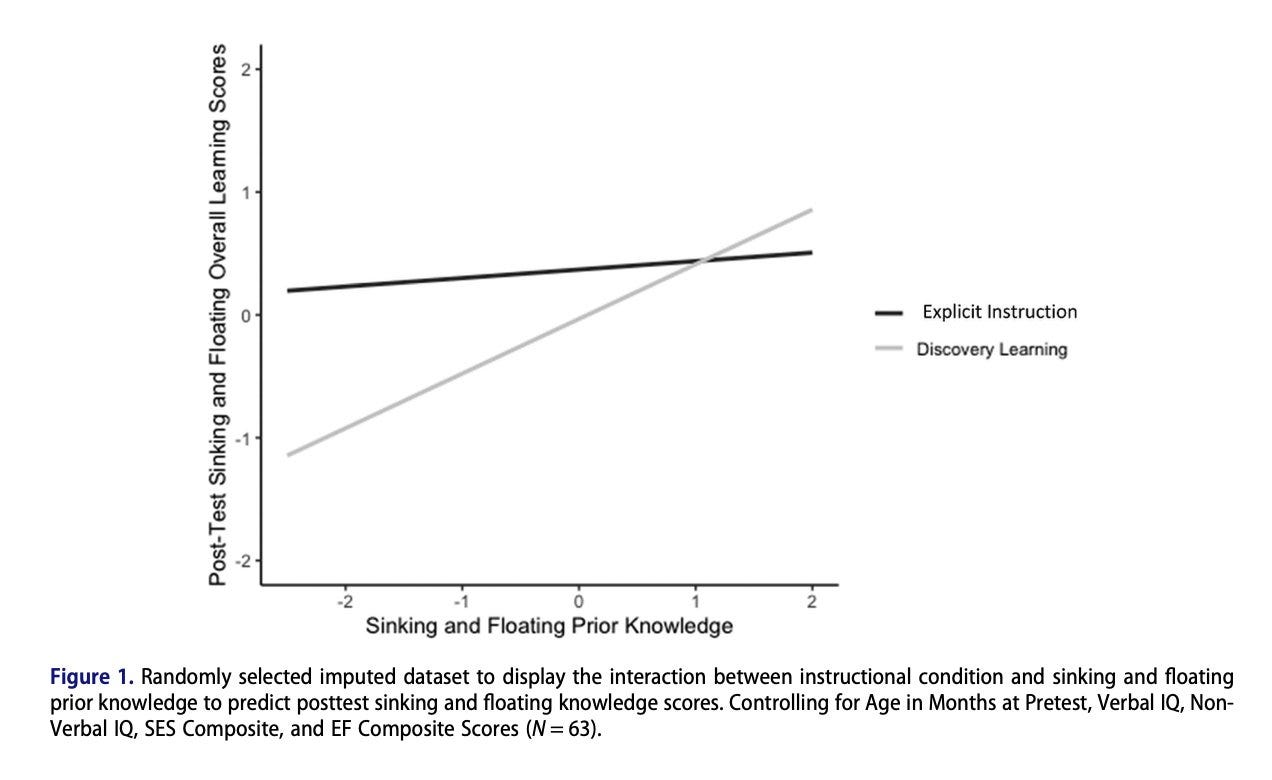
Here is an interesting paper that is good context for the expert/novice distinction. It's called "Preschool Children’s Science Learning: Instructional Approaches and Individual Differences" by Grenell et al. The key figure is here:¹

This is another paper in the vein of the expertise reversal effect. Students with less knowledge benefited more from direct instruction, students with more knowledge benefited more from problem solving. What's striking is that these are preschoolers. When someone asks me to picture an expert, I don't picture a preschooler. But being an expert isn't about being an adult, or passing a test, or having a credential. In this case it just means learners who know a bit more about the topic they're trying to learn.

A Different Framing

Here's a different framing that I think is more helpful for teachers:

• If you assume students know something, make sure they know it

• Teach one thing at a time

Here's an example of what I mean. One seventh grade standard is to solve percent increase/decrease problems. A challenge I ran into in the past was that my students didn't know the meanings of the words increase and decrease. I teach a lot of students for whom English is their second language, and some students who speak English at home also weren't familiar with the words. When I first started teaching percent increase/decrease I assumed, without realizing it, that students knew the meanings of the words increase and decrease. It was a mess. I'd be working with a student who was having a hard time, and they'd constantly mix up increase and decrease or forget what we were learning entirely.

Now I am a lot more intentional about teaching those skills separately. Earlier in the unit we practice finding percentages — you have to be pretty good at finding percentages to solve percent increase/decrease problems. A few days before we get to percent increase/decrease I do a mini-lesson on what increase and decrease mean. I give a few examples, have students answer a few questions like "what is 12 increased by 2." A whole bunch of students say 24, we step back and talk about what increase means again, and practice a bit more. Students solve some problems on mini whiteboards. The whole thing takes about 7 minutes. A day before we start percent increase/decrease I review it again, this time with a few simple questions on slides and some choral response. This time it's maybe 3 minutes tops. The point is that this doesn't take tons and tons of time. I don't need to set aside an entire lesson. I do need to teach what increase and decrease mean, give students a few examples, have them practice a bit, and check for understanding.²

Then when we get to percent increase/decrease I do a quick reminder of increase and decrease, and suddenly the lesson goes way smoother than the mess I was in when I first taught this topic. When we do tax and tips and discounts and all that they have a strong foundation with percent/increase/decrease.

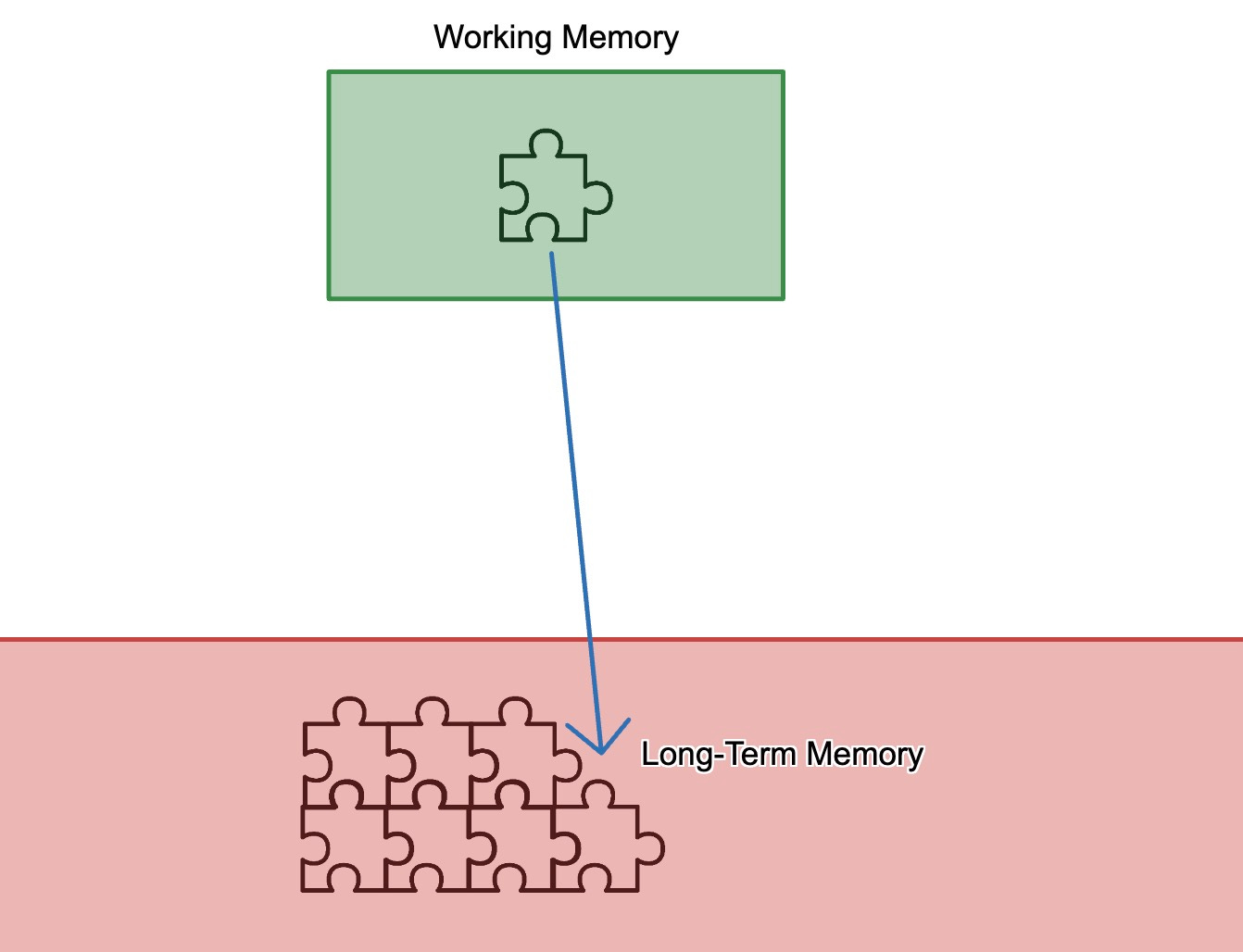
Learning is sticky. Ideas are most likely to stick to something students already know, something that's solidly in long-term memory. It looks like this:

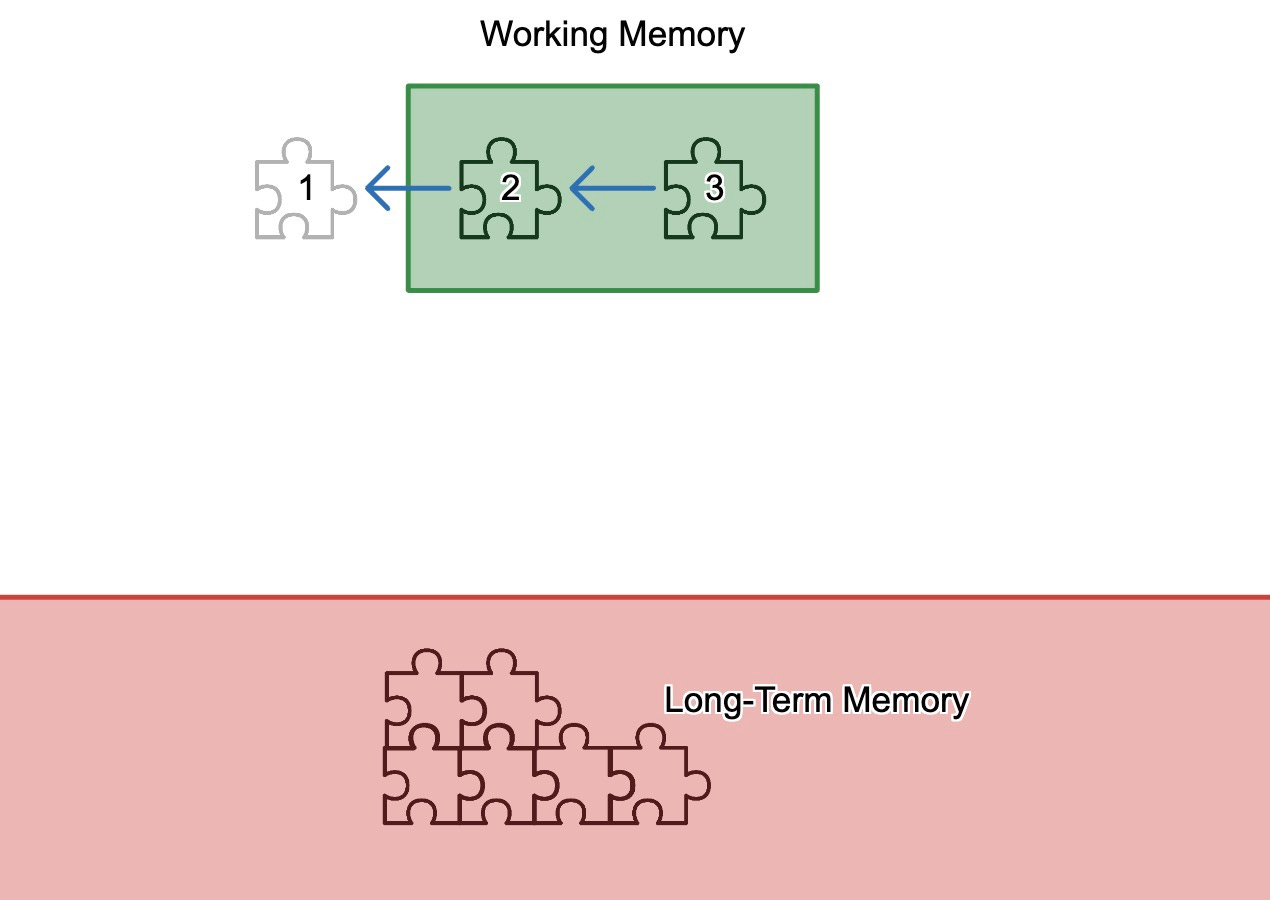
If I try to teach too many connected ideas at once, they aren't actually sticking to anything in long-term memory. Students are trying to hold everything in their working memory, and it doesn't stick to what they already know. That looks like this:

In that diagram I’m trying to teach a few different things at once. They’re connected to each other, but trying to do them all at once means they’re not connected to anything in long-term memory. The first thing never actually made it into long-term memory, the second thing is trying to stick to the first thing, then the third to the second. Then they all fade and nothing is left.

The key to getting this right is to figure out what my lesson assumes students know and make sure they know it, and to teach one thing at a time.

Final Thoughts

I find the novice/expert framing shallow. I can use worked examples with “novice” students and the lesson will still be a mess if I don’t do a good job teaching one thing at a time. The novice/expert framing also doesn’t give me a satisfying answer for why problem solving can fail. It becomes circular: if problem solving fails it must be because the learners are novices, and learners are novices because they don’t learn from problem solving. Instead, I need to think: what does this problem solving activity assume students know, and how will I make sure they know it? Then, once I’ve broken that down into pieces and taught it, students can learn from the problem solving activity. There are plenty of problem solving activities that students do have the knowledge for early in the learning process. I often do a lot of what I would call problem solving early on in a unit as a way of reviewing topics students have already seen and connecting to what I want them to learn. Problem solving fails when it’s trying to do too much at once, or when it tries to build on knowledge that students don’t have.

Words and phrases like "expert" and "novice" and "schema" and "problem solving" and "worked example" mean different things to different people. Teachers need more practical advice. For me, "if you assume students know something, make sure they know it" and "teach one thing at a time" are much more practical. The catch is, they're not easy to do. It's not easy to step back and realize all the little things I assume students know. It's not easy to figure out when one thing is actually two things, but that type of thinking is what helps me to grow as a teacher.

To go back to where I started, I worry that the novice/expert framing communicates to teachers that all students are novices, therefore they should always teach through direct instruction. But problem solving is an important part of math. I want students to apply what they've learned in lots and lots of different ways. That's how they learn to use math beyond the confines of my classroom and to become better problem solvers. The key is to make sure students have the knowledge they need to learn from problem solving.

1. Thanks to Dylan Wiliam for sharing the figure on Twitter

2. As you read you might be thinking, "wait, you said one thing at a time, but it sounds like you taught increase and decrease at the same time, what's with that?" One thing at a time is catchy and concise, but a more precise formulation is "make sure everything you teach is connected to something in long-term memory, and wait until that new thing is securely in long-term memory before teaching the next thing that’s connected to it." I want students to connect "increase" to their ideas of addition and getting larger, and to connect "decrease" to their ideas of subtraction and getting smaller. It works to teach them both at the same time because each idea is connected to something in long-term memory. Then, percent increase and decrease have something solid to connect to. One thing at a time means make sure you don't try to teach A which depends on B, and B which depends on C, at the same time, but you can teach X which depends on Y, and also Z which depends on W, at the same time.