New Research on Prior Knowledge

Commenting on a recent study

A New Study

Thanks to Carl Hendrick for flagging and writing about a new study on prior knowledge. Here's a quick summary:

One common result in cognitive science is that the more you know about a topic the easier it is to learn. A study tested this hypothesis with an experimental design by giving participants 50 minutes of training on a few different topics. Then participants completed readings on topics, some which they had prior training on, and some which they didn't. They then did some additional studying on each topic, and were assessed two days later. If the prior knowledge hypothesis was true, you would expect more robust learning on the topics where participants got an extra 50 minutes of training before learning. But that wasn't the case. There was no significant difference between topics with additional prior knowledge and topics without.

An Example

Carl unpacks some of the potential flaws in the study at his (paywalled) blog and this Twitter thread. I want to dive a bit deeper into this with a specific example, and a mental model to guide thinking around prior knowledge.

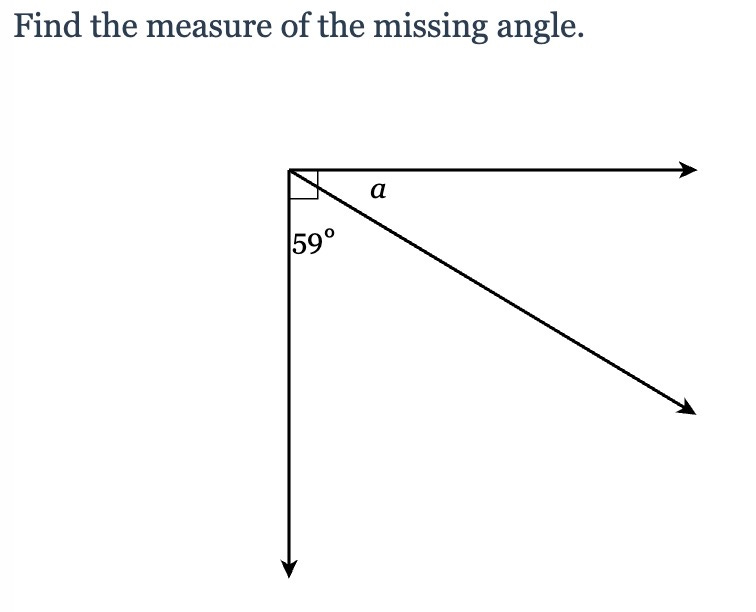
One topic I teach is complementary angles. A simple question looks like this:

Gradually we get to more complex questions with multiple angles, supplementary and vertical angles mixed in, and more, but we start with questions like the one above.

There are three pieces of knowledge that are really important to help students understand complementary angles. First, they need to know that a right angle measures 90 degrees. Second, they need to have a broader intuition for angle size in general. Third, they need to know how to solve an equation of the type x + a = 90. Before I teach complementary angles, I spend time reviewing those topics. Importantly, I do this over a number of classes in lots of small chunks. We might do some problems on mini whiteboards where I ask students to draw a 90 degree angle, or solve x + 35 = 90. I gradually ask students to do more and more varied tasks, especially with right angles, to build connected knowledge around what a right angle means. Draw an 80 degree angle. Draw a 20 degree angle. Draw a quadrilateral with exactly one right angle. Estimate the size of this angle that's a bit larger than 90 degrees. Solve x + 35 = 90, then find 90 - 35, and understand that the answers are the same. I mix these in to Do Nows and other quick chunks of practice, often on mini whiteboards. The goal is for students to have a broad understanding of these ideas and lodge them firmly in long-term memory before I teach complementary angles. It's worth noting that these topics are prior year standards so students have seen these before, but that doesn't mean I can assume students know it. I don't do this right before the lesson on complementary angles. I start a week or two before, and mix these mini-lessons and problems in with other topics.

When I do this well, complementary angles just make sense to students. I introduce the topic, and it's almost like students say "well of course they add up to 90. What else would they add up to? It's 31 degrees, duh."

What Does Prior Knowledge Do?

Returning to the paper, I think it's worth reframing "prior knowledge facilitates new learning." Here are two principles that I find more valuable:

• Teach one idea at a time

• Connect each idea to something in students' long-term memory

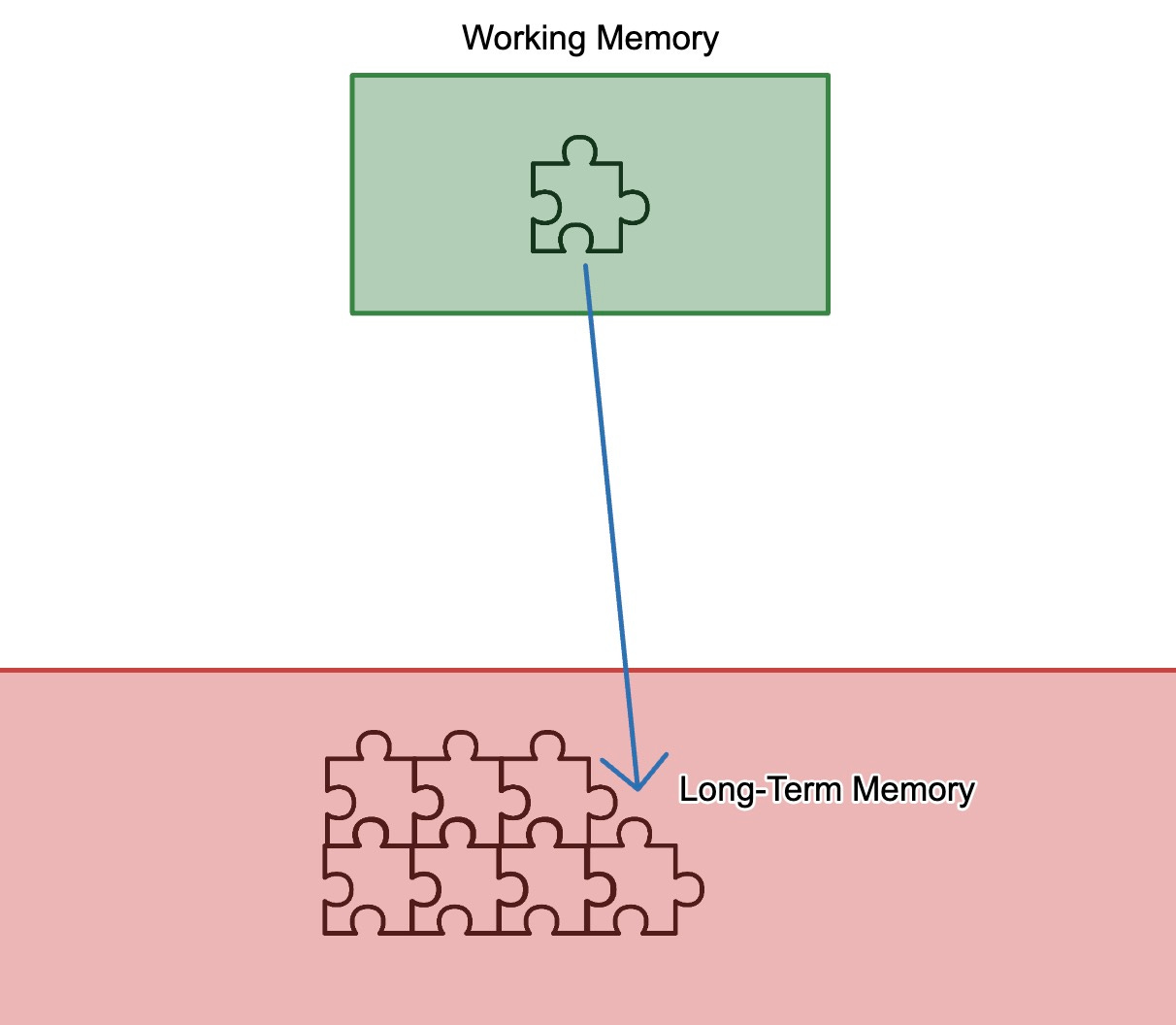
Here's a model of effective learning:

Students think about something (working memory is where thinking happens). They connect that thinking to other ideas they already have in long-term memory. It's important that this is precise. It's not like "students know some things about angles, so it's easier to learn more things about angles." Random puzzle pieces floating around don’t do much to help learning. There are very specific pieces of knowledge students need. That's one flaw in the study: the prior knowledge wasn't precise. It was "ok, learn some things about this topic, then learn some more things about this topic." Those puzzles pieces have to line up and connect, not just get tossed together willy-nilly.

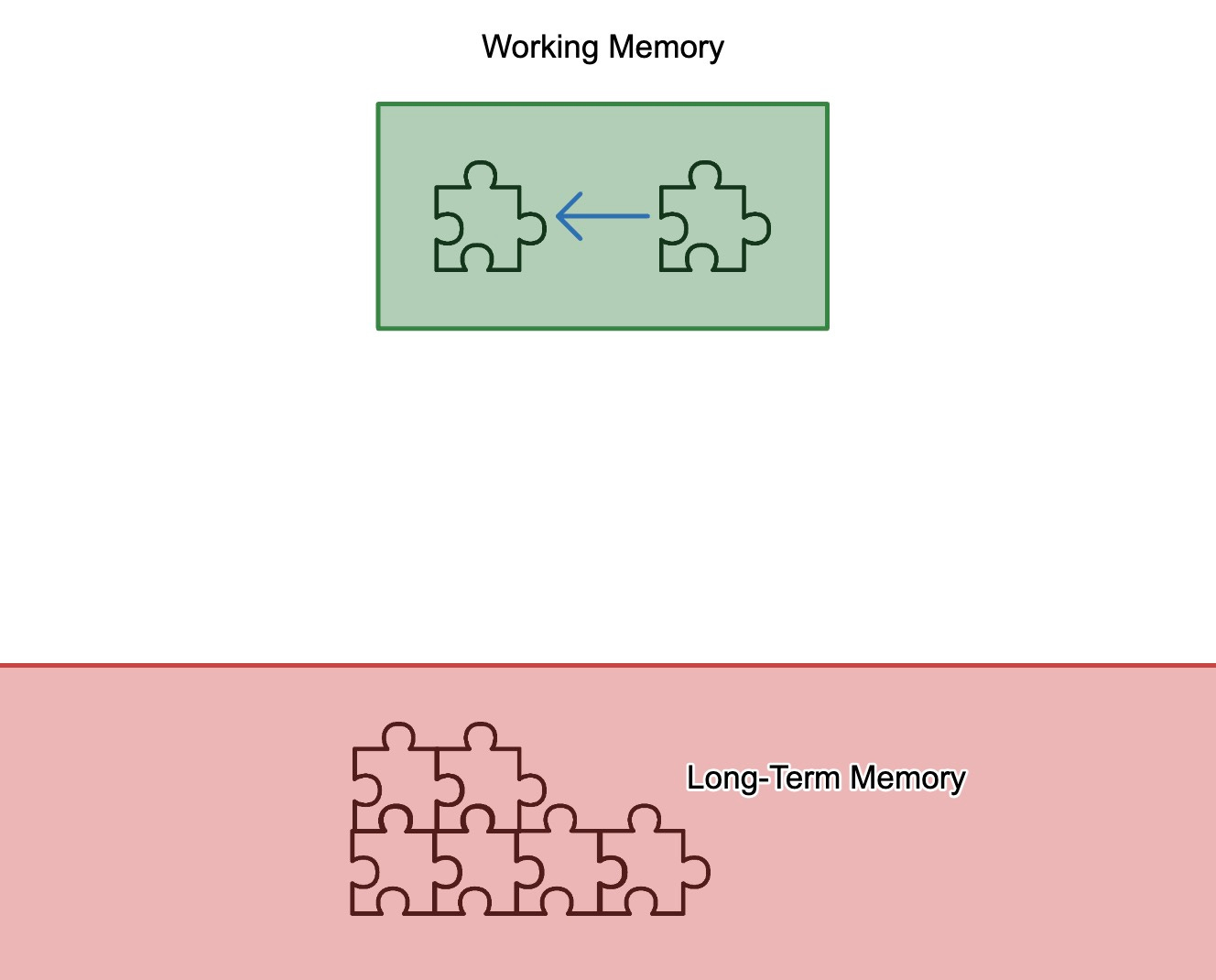
Here's a model of ineffective learning:

If students don't have the meaning of a right angle firmly in long-term memory, I'm trying to teach multiple things at once. I'm connecting the things that students are thinking about, but not connecting that thinking to knowledge in long-term memory. This is a recipe for shallow learning and fast forgetting.

Returning to the study, the researchers only had participants study a "prior knowledge" topic for 50 minutes — probably not long enough to create a strong long-term memory. They also weren't very intentional about the connections between prior knowledge and new learning. This isn't to say the study is bad — it's a good study, and an important reminder. There's a bad way to do prior knowledge that begins a lesson by saying, "Hey kids, remember what a right angle is? Great, let's learn about complementary angles." That's not likely to help. Or, more precisely, some students will have a strong memory of right angles and will do well, others won't have that memory and will struggle, and the quick review of prior knowledge won't make much of a difference. Prior knowledge should be specific, targeted, and clearly connected to what we want students to learn next. It should also be firmly embedded in long-term memory to facilitate those connections.

I'm cherry-picking here. Complementary angles are a pretty simple topic to teach, with clear and well-defined prior knowledge that students need. I also teach proportional reasoning. 7th grade proportional reasoning draws on knowledge of multiplication, division, the inverse relationship between multiplication and division, unit rates, equations, coordinate planes, knowledge of specific contexts like money and distance and time, and more. Most topics students learn in school are more like proportional reasoning. There’s a broad and complex network of prior knowledge that’s connected to what we want students to learn.

For each topic, I want to think about two principles. First, I want to make sure I’m teaching one idea at a time. If students don’t know something I assume they’ve already learned, I’m probably teaching two things at once. That doesn’t work very well. And second, I want to be really specific about how the idea I want students to learn is connected to other ideas they already know. What specific ideas is it connected to? How can I make sure students already have that knowledge firmly in long-term memory and make those connections? For most content I teach, the amount of prior knowledge students might need can feel overwhelming. By focusing on those two principles, I can focus on a few manageable, targeted pieces of prior knowledge.