Memorization Done Well

Not just drill and kill

“It’s important for students to memorize math facts.”

That statement is a bit of a Rorschach test for math teachers. Some teachers will assume that I care about regurgitation over understanding, that I think there’s nothing more to math than memorizing things, and that I endlessly drill students on facts day after day. Others will jump right to mad minutes and assumptions about speed. Some will acknowledge memorization is important but look at it like the unappetizing vegetables of math education. But all of us are often imagining very different classrooms based on our own reaction to the word “memorize.” It’s worth being specific. What do I mean by “memorize”? What needs to be memorized? What is the best way to help students memorize things?

What Do I Mean by “Memorize”?

When I say “memorize” I mean “know from memory without having to think about it.” Humans can only think about a few ideas at a time without becoming overwhelmed or losing track of something. Having facts memorized makes thinking about hard stuff easier. The magic of this process is that we don’t realize it. Every time we think, we rely on skills and knowledge that we take for granted but are essential to free up space in our minds.

Here are two things I don’t mean when I say memorize. I don’t mean “know in a narrow, inflexible way that can’t be applied in unfamiliar situations.” I want students to memorize that 4 times 5 is 20. But I also want them to know that 20 divided by 5 is 4, and how to solve 4x=20, and that 4 times 5 must be twice as big as 2 times 5 and more. There’s no contradiction here. Students can memorize facts and think flexibly. One doesn’t impede the other.

I also don’t mean “learn through endless drill and repetition.” To some people, “memorize” describes a way of learning something. Memorization isn’t repeating the same thing over and over again or completing endless repetitive worksheets. I’m not advocating for any of that.

Finally, some people will split hairs about the difference between memorization, automaticity, fluency, and all sorts of other things. I realize that there is disagreement about the meaning of these words. I like my definition, and the word memorization, because I think they are intuitive for people outside of education. It’s helpful to use words that aren’t jargon whenever we can.

What Needs To Be Memorized?

Last week I was teaching students how to add integers. I asked students to analyze a worked example solving -4 + -6 = -10 on a number line. I asked students, "How is -4 + -6 similar to 4 + 6?" I wanted them to understand that adding two negative numbers is the same as adding two positive numbers, only the answer is negative. We also use number lines and a floats and anchors representation for working with integers, but knowing the rule for adding two negatives becomes helpful when they have to keep adding negatives, subtracting negatives, and multiplying negatives straight in their heads.

That whole example was probably clear to you, dear reader, because I bet you know from memory that 4 + 6 = 10. You didn’t have to think about it. Because you didn’t have to think about it, you were able to make the connection that 4 + 6 is similar to -4 + -6. But if a student doesn't know that 4 + 6 = 10 — if they have to work it out in their head or on their fingers — it becomes hard for them to make that connection. Trying to add 4 + 6 and also make the connection to the example is too much to think about at once, and students who don't have that fact fluency will struggle.

I often hear people say that we don’t need to know math facts anymore because we have calculators. And sure, calculators are great for lots of things. But math facts are the tools for learning more complex mathematical ideas. Not having those tools makes all that other learning much harder. Here’s a second example:

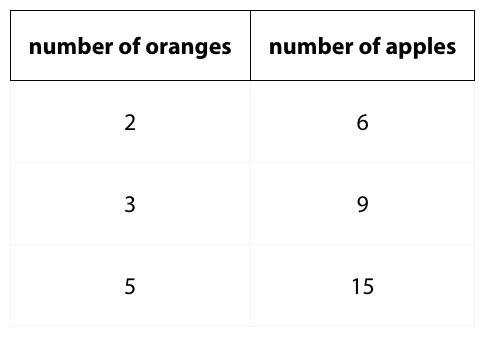
This table comes from the lesson in my curriculum that introduces proportional relationships. The curriculum could have chosen to use a context where 2 orange cost $3.64, 3 orange cost $5.46, and 5 orange cost $9.10. But it’s hard to divide those numbers using a calculator, hold all the answers in your head, and process what it means to be in a proportional relationship. A student who knows their math facts will have way less to think about looking at this example, and will be much more likely to understand the meaning of a proportional relationship.

That’s my answer to the question, “what needs to be memorized?” Knowledge that frees up space so students aren’t thinking about as much as they try to learn new things. Basic math facts fall into that category. Same for knowing the coordinate plane while doing all sorts of things with graphs. Knowing how to find equivalent fractions when working with slope. Knowing how to solve one-step equations when moving on to two-step equations. There’s plenty more. I don’t think it’s important to memorize how to complete the square, or how to find mean absolute deviation, or the Taylor series error formula — knowing those doesn’t free up space the same way.

What Is the Best Way to Help Students Memorize Things?

Retrieval practice. Retrieval is the best way to solidify knowledge in long-term memory. But I worry that even people who think they are well-acquainted with retrieval practice focus too much on “practice” and not on “retrieval.” Retrieval means that the student is reaching into their memory to remember relevant knowledge.“Rehearsal” is when the teacher tells the student something and gets the student to think about it. Rehearsal is one important part of learning, but if I want students to memorize things I want them to move away from rehearsal to retrieval. Lots of things that look like retrieval are actually rehearsal. Here are some things that aren’t actually retrieval practice:

• "Remember, to divide fractions you flip the second fraction and multiply. Try the first five problems on the handout." — Students aren't retrieving what they know from memory, they're doing what you told them to do.

• "Ok, you're trying to divide fractions. Where in your notes did you write how to divide fractions?" — Students aren't retrieving, they're getting that information from an external source.

Here are some things that do involve some retrieval, but aren’t as effective as you might think they are:

• “Here’s your mad minute. Solve as many as you can in 60 seconds. Go.” — Students are doing some retrieval practice, but many are retrieving the facts they already know and skip-counting for the facts they don’t. This doesn’t provide retrieval practice on the facts they most need to learn.

• "Let's read the problem. What are you trying to do? Divide fractions, right. What’s the opposite of division? Multiplication, right. How might you use an opposite to solve this problem?" — Students might do a bit of retrieval here, but it's so heavily cued by the teacher that they aren't getting the full benefit from thinking through what the problem is asking and retrieving from memory.

• "Here are fifteen problems in a row on this topic, get to it!" — The issue here is that students are probably only retrieving once at the beginning, then doing the same thing over and over again.

• "Here's a giant project that involves solving one fraction division problem but also lots of critical thinking." — This could be fun I guess. But students are only retrieving how to solve the problem once, if that.

Retrieval practice happens on two levels. First, within any one chunk of practice, how often are students retrieving knowledge? If students are repeating the same thing over and over again they are rehearsing not retrieving. If students don’t know something they aren’t retrieving, they’re grasping at straws. I love using mini whiteboards to facilitate retrieval because I can adjust as I go. Let’s say I want to work on fraction division. I can remind students how to divide fractions and give them a quick problem to rehearse what to do. Next I give them a simple problem on another topic they know how to do. Then, a new fraction division problem — this is retrieval. If it goes well, I mix in two different problems students know how to do and then more fraction division. If students have a hard time, I take a step back and figure out how to help students understand the concept. If they do well I continue the mixed practice. I can do more in ten problems of focused practice than thirty repetitive problems. Mini whiteboards aren’t the only way to do this. You can do it on paper or digitally, lots of different ways. But being able to adjust to what students know and don’t know is really helpful in facilitating successful retrieval.

The second level of retrieval practice is spacing over time. I want students do some retrieval within a single lesson. I also want students to retrieve that knowledge tomorrow, the next day, twice next week, once the week after that, once next month, and so on. Short-term retrieval is what create a strong initial memory. Long-term retrieval helps students retain it for the long run.

A final note on retrieval: none of this requires putting time pressure on kids. Speed is one proxy for having things memorized, but timing kids doesn’t magically make them faster. Well-structured retrieval practice is much more effective than putting a timer on the board.

Coda

I want to reiterate the core ideas of this post:

• Memorization means knowing something without having to think about it

• Memorization is important when it frees up space to think about more complex ideas

• The best way to memorize things is retrieval practice, which means getting students to retrieve knowledge from memory as much as possible

There’s more to math than memorization. That’s part of the point. Some people think that if a teacher cares about memorization they must give students endless “drill and kill” practice or whatever. And some teachers do! But the reason they spend so much time on it is because that repetitive practice is an inefficient way of committing knowledge to memory. Effective use of retrieval practice helps students memorize ideas efficiently, freeing up time for all the other stuff that’s important in math class.

I also haven’t touched on how to introduce students to new ideas. Some people were probably yelling through the screen at me about fraction division. “They’re just memorizing without understanding!” I’m not saying that when students initially learn fraction division they should memorize “flip the second fraction and multiply.” They should connect fraction division to what they already know about fractions and division. But anyone who has taught middle schoolers knows that, no matter how well students understand it initially, some will forget and need to be reminded. That’s what retrieval practice is all about — making the learning stick, so that when we work on unit rates with fractions the fraction division part is easy.

Finally, I haven’t circled back to flexibility. I want students to be able to solve problems flexibly, to use what they know in different ways, and to transfer knowledge to new contexts. Having some knowledge memorized can help with that! But if practice is always the same, students will never have the chance to apply that knowledge in different ways. I’m not going to go into depth on this point, but this is another argument against practice that is too repetitive. Memorization is important, but memorization doesn’t mean endless repetition. Pure repetition isn’t the best way to memorize things, and it also doesn’t help students to apply their knowledge flexibly.

Teachers shouldn’t be afraid of memorization. We should understand when memorization is important, do it well, and make time for everything else we want to do in math class.