An Illustrative Mathematics Curriculum Review

Lots to love and one place it falls short

This is my third year teaching the Illustrative Mathematics (IM) 7th grade curriculum. Overall I like it. It does a lot of things that curriculum should do, that are hard to do if you're patching stuff together yourself. The sequencing from beginning to end is thoughtful. There are a wide variety of question types that push students to apply the content in lots of different ways. The representations are thoughtfully chosen and developed. The routines and structures that repeat throughout the curriculum help students get used to different ways of thinking and also free up thinking space for challenging content. The examples are well designed.

But there's one thing that's been bugging me, and that's been driving a lot of the modifications I've been making to the curriculum. (By the way, a bonus of using open source curriculum is that it's easy to remix and modify the materials.) IM takes an approach that I'll call "they just need to really understand it." The philosophy says that if students truly get something, if it fits in their mind, if it connects to their prior knowledge and builds off what they've already learned, that's enough to remember it and be able to solve problems with it. I'm going to try to illustrate that idea with a lesson I just taught.

One Lesson

The lesson is meant to introduce writing equations of the form y = kx to represent proportional relationships. We've solved a bunch of proportional reasoning problems using tables as our major representation but haven't introduced equations yet.

The lesson starts with a number sense warmup, then jumps into this activity.

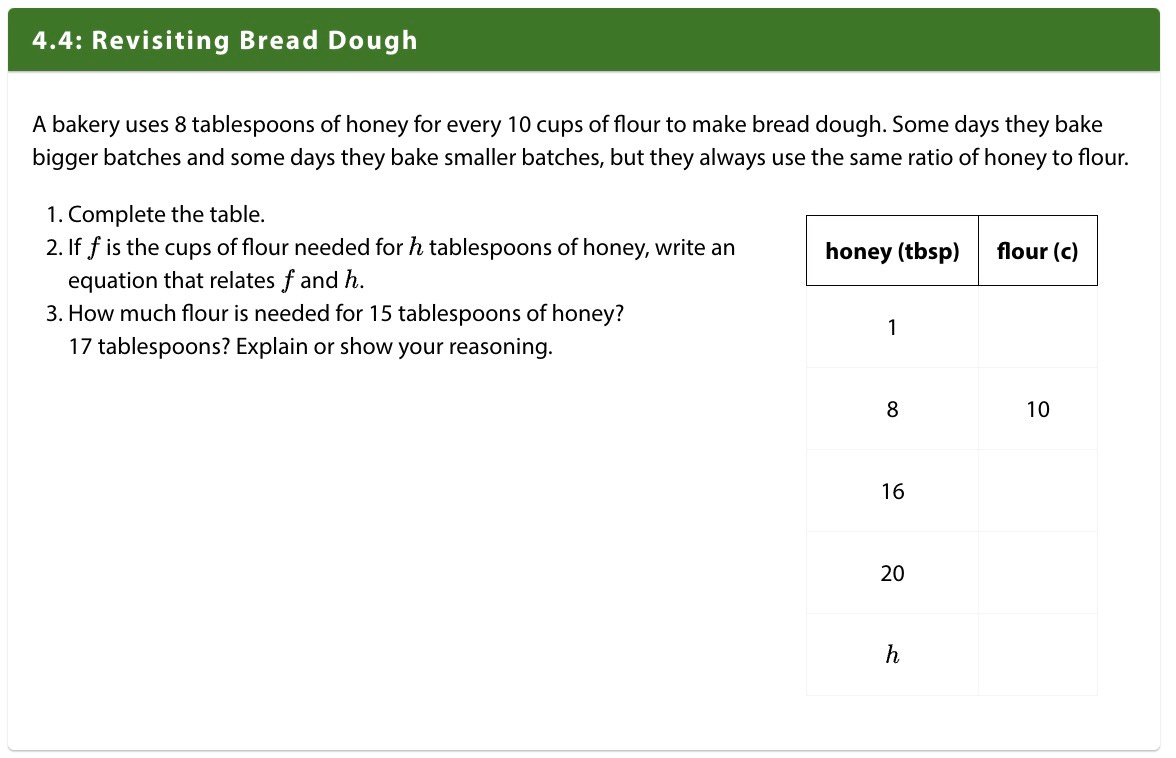
Both contexts and some of the numbers are repeated from an activity from a few days ago. I love this choice, along with the way the numbers work out well — students are mostly confident filling out a table like this, and because the example is repeated we can focus on the added wrinkle of the algebra. Here students aren’t writing full equations, but they are thinking about what the expression 3x or 0.5n means in this context.

Next comes this activity.

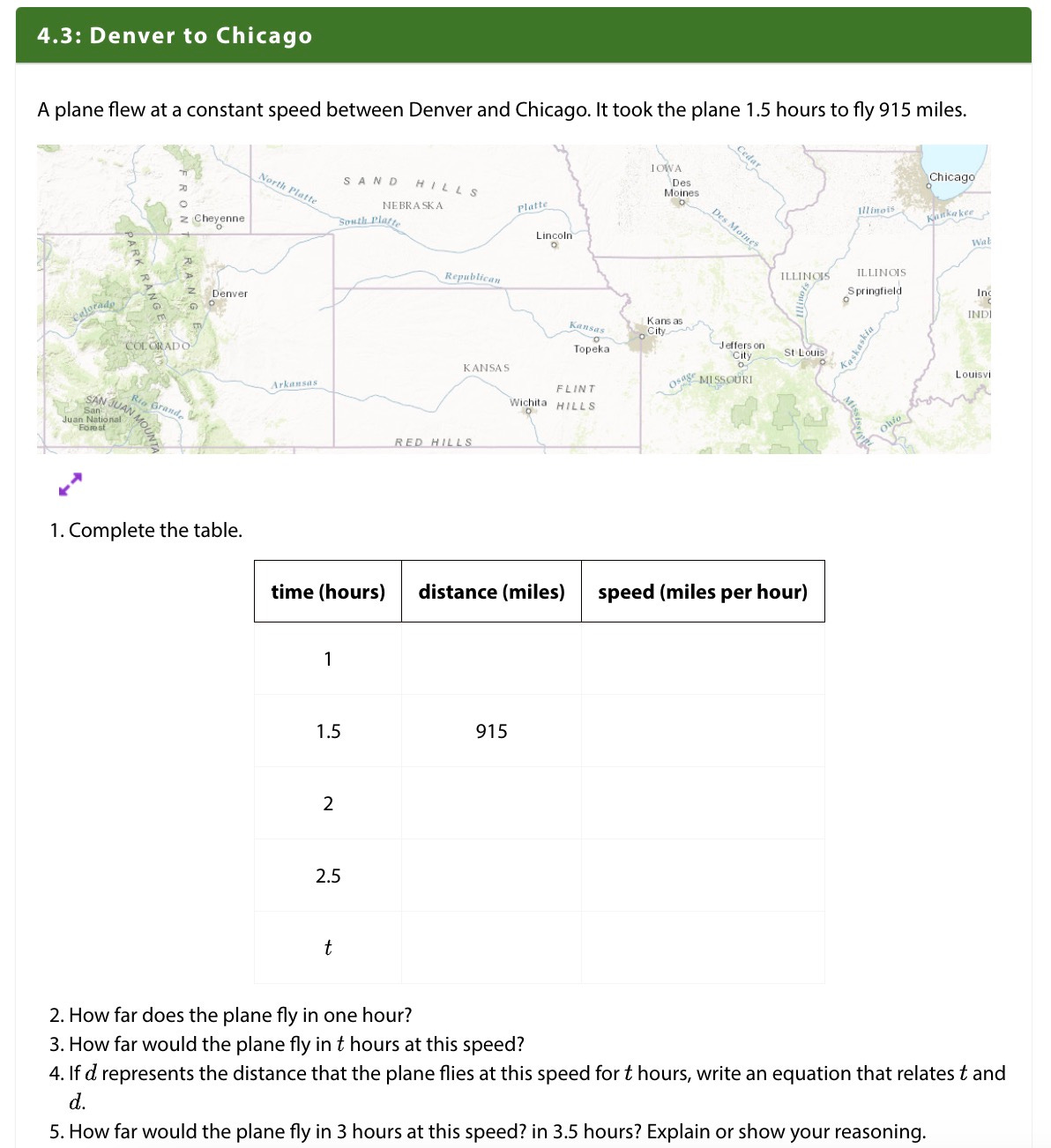
This one is hard! But I like the choice to include a speed/distance/time context and to emphasize the role of the constant speed, which is also the constant of proportionality and k in the equation. Another good move is to choose numbers that require a calculator; it's good for students to have to divide to find the constant of proportionality and not only try problems where they can "see it" from the context. Here they also take the step of writing a full equation, rather than just an expression, and then using it to solve some extra problems not in the table.

The last activity also repeats an earlier context.

The numbers don't work out nicely, but that builds well off the last activity. Many students can fill out the table independently at this point, though the equation takes some scaffolding for most students.

The Review

This lesson does a lot of things well. All those activities are good! It's a good lesson. But there's a tough skill in here, and this one lesson isn't enough to get students good at it. The skill I want students to be good at is writing an equation for a proportional relationship. This is a counterintuitive piece of math. Imagine students are writing an equation for the number of legs (l) possessed by a certain number of horses (h). A reasonable 7th grader might say, "oh that must be h = 4l, because each horse has 4 legs." But that's backwards, I want them to write l = 4h, meaning to get the number of legs you have to multiply the number of horses by 4. All the activities above are great. They help students understand where equations come from, why they might be useful, and how they connect to their previous knowledge about tables and proportions. What they don't do is give students a bunch of chances to apply their knowledge, test its limits, and refine their intuition for writing equations.

To be fair there are a few practice problems at the end of the lesson. You can see them here. I don't find them helpful as practice here because they're not granular enough. Students never have to write an equation from scratch; one variable is always given, or they are interpreting an equation that’s written for them. There's a very specific skill here that is hard, that students haven't practiced enough, that students need a bit of guidance to start but will hopefully develop independence with. That skill is being given a relationship, like 12 inches in a foot, and writing an equation for the relationship using f for feet and i for inches. The practice problems have too many moving pieces, and it's easy to lose the thread of that key skill.

This is also a long lesson! I didn't have much time at the end. But at the start of next class we revisited this same topic, and we did a bunch of quick, focused, practice on mini whiteboards writing equations. We started with the scaffolding of a table for situations like 1 starfish has 5 legs, 3 starfish have 15 legs, what’s an equation relating starfish and legs. Then inches in a foot. Then jalapeños in nachos because one student loves nachos. Then I took away that scaffolding. It's a hard skill! And it's not a knock on the activities that students didn't perfectly understand it. It’s not like students were perfect after my focused practice. But they made a ton of progress, and we did a bunch of turn and talks and quick share outs to practice explaining why the equation is i = 12f and not f = 12i. My knock is that the curriculum doesn't design this kind of granular practice into their approach.

Zooming Out

I believed this mindset for a long time. And the thing about the "they just need to really understand it" mindset is that it's an infinite regression. If the lesson doesn't go well I can say, "ok they didn't really understand it, I need to go deeper." I've seen this type of thinking from lots of other teachers too. We constantly want to invent a better explanation, sequence a better series of problems, facilitate a better discussion. And sure, that can be valuable when the understanding isn't where it needs to be. But there are also situations where the understanding is fine, and what students need is some focused, guided practice.

That type of practice is what I've been adding to the IM curriculum, and it's made a huge difference for me. Kids are happier — they feel frustrated when they don't remember something the next day. It’s not fun to feel like you understand something in the moment but it doesn’t stick and the next day you forget. I'm still able to take advantage of all that thoughtful sequencing and coherence. And a lot of these chunks of practice are only 5-10 minutes. I'm not talking about blowing up the whole thing, though I do often get rid of an activity and replace it with some practice I've designed. Sometimes it's improvised on mini whiteboards, sometimes its on paper, sometimes its a mini lesson and a targeted DeltaMath skill. Practice doesn't need to feel dry and doesn't need to be 30 problems in a row. A little bit of extra, focused work at the right moment for key skills makes a huge difference.

I think this is a decent review of the IM curriculum as a whole. There's lots to love. It really prioritizes thoughtful sequencing and building up student understanding. That stuff is great. What's missing is the targeted practice to make sure students retain that understanding for the long haul.