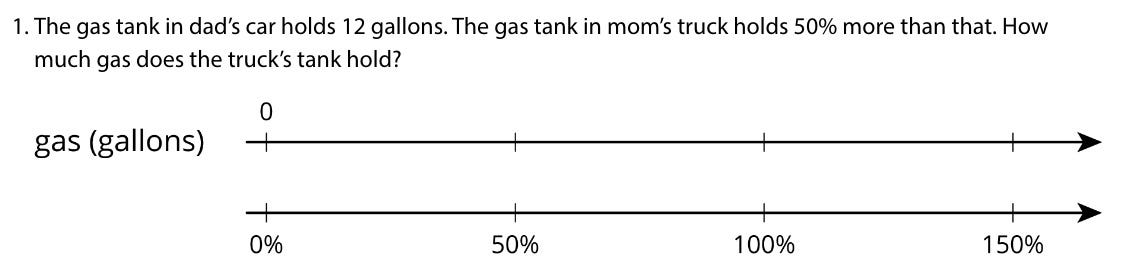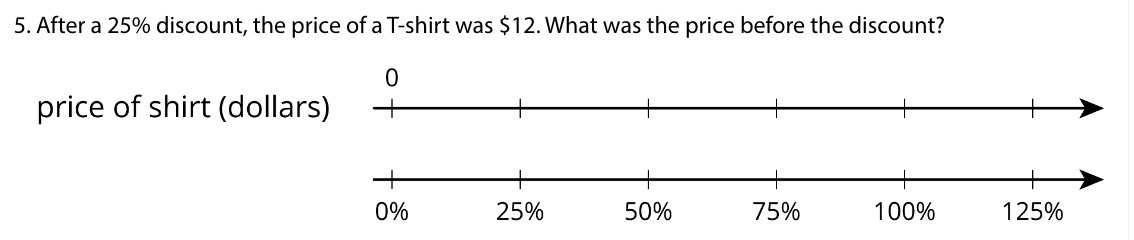A Nice Worksheet
And a short rant about how worksheets are unfairly maligned
Worksheets are just pieces of paper with math problems on them. The specific problems and the way they fit together can be good or bad. Students can be prepared or not prepared to learn something from those problems. They can be used by teachers in ways that support or hinder learning. People who talk about teaching focus too often on the surface features of what's happening rather than the substance. If I'm giving students problems on whiteboards I'm progressive or I value student-centered learning or the whole child or something. If I'm giving students problems on paper I'm a boring old traditionalist. That's silly. We'd be better off focusing more on the thinking students are doing, and less on the paper problems are printed or not printed on.
Anyway, here's a worksheet I used last week. (link)
Take a minute to look at the problems. I think it's a nice little worksheet. I designed it using the ideas of variation theory, trying to change as little as possible from one problem to the next. This structure can help students who are less confident, because they can better use their thinking from the last problem to help them on the current one. It can help students make better inferences about cause and effect as one part of the problem changes, encouraging deeper thinking about what's going on. And it can create opportunities for students to find shortcuts by using the structure of one problem to figure out the next one. The worksheet led to some great conversations about how percents are commutative — 30% of 50 is the same as 50% of 30, etc. It also led to some great conversations about how to scale percents proportionally, in particular questions 11 to 15 where some students were hesitant to find 1,000% of something but could see the pattern from the previous problems.
The other thing that was nice about this worksheet was how students responded to it. The first part of class we were working on this lesson in the Illustrative Math curriculum. The core of the lesson is a series of problems like this one:
Or this one:
These are hard! I was asking kids to do a lot of hard thinking. It's good thinking, and helpful to have a concrete representation of percent increase/decrease to fall back on as we transition to solving them more abstractly. But it’s still hard. I actually planned to use the worksheet a previous day but we didn't get to it. I kept it around and when I realized the lesson wasn’t going very well I cut the final activity and pulled out the worksheet. A bunch of students felt discouraged and hadn't been participating very actively in the double number line problems. When I passed the worksheet out, most students got right to work without hesitation. I was able to get the rest started without too much trouble. The whole atmosphere in the room changed. Students had been kindof grudgingly working on the double number lines with a lot of prodding from me as I ran around. Suddenly they were focused and grinding on the worksheet. There's something about a worksheet that can feel safe and predictable. This one also has a nice on-ramp of accessible questions for students to start with, to help them build some confidence early on before getting to some trickier problems.
I have two points with this post. First, worksheets are often unfairly maligned. Worksheets are just pieces of paper with math problems on them. There's nothing wrong with giving students a worksheet. Worksheets become a problem when there's too much repetition and students stop thinking, or when they're the only pedagogical tool a teacher uses. This worksheet balances a bit of practice with opportunities to notice patterns and find shortcuts. And second, some activities in math class require a more cognitive energy than others. A worksheet can be a pleasant change of pace when students are mentally tired. This wasn’t in service of the lesson objective or anything, it was a chance for some practice, maybe some new understanding, and for students to feel successful on a task before the end of class after doing some hard thinking.